www.mundonano.unam.mx | Mundo Nano
http://dx.doi.org/10.22201/ceiich.24485691e.2022.29.69707 | 15(29), 1e-14e, julio–diciembre 2022
Artículos de investigación
Análisis de las propiedades vibracionales del crotonaldehído: DFT vs MD◊
Analysis of the vibrational properties of crotonaldehyde: DFT vs MD
Ricardo Ruvalcaba*
Jonathan Guerrero-Sánchez*♦
Noboru Takeuchi*
* Universidad Nacional Autónoma de México, Centro de Nanociencias y Nanotecnología, Ensenada, BC 22860, México.
♦ Autor de correspondencia: guerrero@cnyn.unam.mx
Resumen:
La dinámica molecular (MD, por sus siglas en inglés) y la teoría del funcional de la densidad (DFT, por sus siglas en inglés) son actualmente las teorías más utilizadas en ciencia computacional de materiales. Ambas tienen alcances y aplicaciones distintas, pero convergen en ciertas áreas. El presente trabajo hace una comparación y contraste entre la exactitud de ambas teorías para modelar el espectro infrarrojo de una molécula orgánica sencilla pero representativa: el crotonaldehído. Se lleva a cabo un análisis de las energías, distancias de enlace, frecuencias e intensidades vibracionales para determinar las ventajas y desventajas de cada teoría en este marco de cálculo.
Palabras clave: espectro infrarrojo, teoría del funcional de la densidad, dinámica molecular.
Abstract:
Molecular dynamics (MD) and density functional theory (DFT) are currently the most widely used theories in computational materials science. Both have different scopes and applications, but they converge in certain areas. The present work makes a comparison and contrast between the accuracy of both theories to model the infrared spectrum of a simple but representative organic molecule: crotonaldehyde. An analysis of the energies, bond distances, and vibrational frequencies and intensities is carried out to determine the advantages and disadvantages of each theory in this calculation frame.
Keywords: infrared spectra, density functional theory, molecular dynamics.
Recibido: 2 de noviembre, 2021.
Aceptado: 12 de enero, 2022.
Introducción
Un grupo de compuestos orgánicos de mucho interés para la industria química es el de los aldehídos α, β-insaturados. Estos representan un grupo de sustratos desafiantes para las reacciones de hidrogenación quimioselectiva, donde ambos grupos -CH = O y -C = C- coexisten en una molécula (Gallezot y Richard, 1998). Los productos deseados son los alcoholes (correspondientes a la hidrogenación del grupo carbonilo), pues se emplean ampliamente en la fabricación de perfumes, aromatizantes y productos farmacéuticos (Zhang et al., 2020).
Más específicamente, el (E)-but-2-enal (conocido comúnmente como crotonaldehído) es uno de los aldehídos α, β-insaturados más sencillos que existen. Este tiene como fórmula semidesarrollada CH3CH = CHCHO y se encuentra en 4 isómeros distintos, dados por la posición relativa de los grupos aldehído y metilo, como se muestra en la Figura 1. El crotonaldehído es un compuesto de vital importancia para varios tipos de industria. La Agencia para Sustancias Tóxicas y Registro de Enfermedades (ATSDR, s. f.) reporta que se usa como agente de advertencia en gasolinas, desnaturalizante de alcoholes, preparación de aceleradores de goma y bronceado de cueros. En la industria de química fina se usa para la manufactura de butanol, butiraldehído, metoxibutiraldehído, ácido maleico, ácido crotónico y alcohol crotílico, por mencionar algunos; pero encuentra su uso principal en la manufactura de ácido sórbico (PubChem, s. f-a). En la industria de polímeros, se usa para manufacturar resinas, acetales de polivinilo y como solvente para cloruro de polivinilo. También se utiliza en la preparación de insecticidas, fertilizantes y saborizantes (PubChem, s.f-b).
Figura 1 Isómeros del crotonaldehído. No se diferencian los dobles enlaces entre C1 = O ni C2 = C3. Las esferas blancas, cafés y rojas representan átomos de H, C y O, respectivamente.
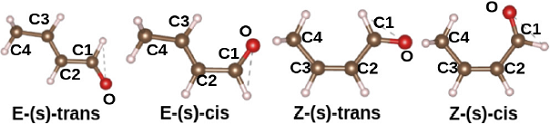
Fuente: Elaboración de los autores.
La simulación de dinámica molecular (MD, por sus siglas en inglés) proporciona la plataforma más fundamental y flexible para el análisis de interacciones moleculares. Los cálculos de MD modelan las interacciones entre átomos mediante las ecuaciones de Newton de mecánica clásica, lo cual puede representar un problema conforme uno se acerca al régimen cuántico. También está reportado que pueden surgir dificultades en la aplicación de condiciones de frontera y en el cálculo de interacciones de Coulomb de largo alcance (Lee et al., 2012). Por estas razones, no es raro el uso de métodos alternativos para buscar modelar las interacciones moleculares.
Como alternativa a la MD clásica, se pueden usar campos de fuerza empíricos creados a partir de mediciones experimentales (Leach, 2001), o se pueden usar otros métodos derivados de la ciencia computacional como el método Monte Carlo (Rogge et al., 2019; Honorio, 2019) o algoritmos genéticos (Bhoskar et al., 2015) para el estudio de las propiedades moleculares. Pasando a teorías basadas en la física y química cuántica, existen toda la familia de métodos tipo Hartree-Fock y post-Hartree-Fock (Magnasco, 2013. Entre estos se encuentra la teoría funcional de la densidad (DFT, por sus siglas en inglés), que es sin duda una de las teorías más utilizadas (si no es que la más utilizada) en la simulación computacional de materiales en la actualidad. DFT se basa en los postulados mecano-cuánticos de Hohenberg-Kohn y Kohn-Sham, que utilizan la densidad electrónica como variable principal para los cálculos, y a partir de la cual se obtienen todos los parámetros de interés del sistema en el estado base (energía, fuerza, etc.). Siendo así, la DFT es la más versátil y eficiente de las teorías cuánticas para modelar materiales. No hay duda de que en sistemas a escala atómica (unos cuantos nanómetros) DFT es una mejor opción que MD. Cuando uno se acerca a la meso y macro escala uno puede seguir usando DFT para obtener resultados con la gran precisión y exactitud que nos permite la mecánica cuántica, pero a un gran costo computacional, lo cual puede llegar a ser prohibitivo. En general, los cálculos en este régimen no requieren una descripción electrónica tan detallada, por lo que se suele recurrir a MD. Es en la frontera entre estas escalas que se pueden utilizar ambas teorías con niveles comparables de costo computacional y (dependiendo de la naturaleza del sistema y lo que se busca estudiar) exactitud en los resultados. Incluso existe el método de Car-Parrinello, que se puede considerar como un híbrido entre MD y DFT (Car y Parrinello, 1985). Asimismo, existen algunos artículos (Qin et al., 2010; Oukhrib et al., 2021) en los que se aplican ambos niveles de teoría a un mismo sistema para estudiar parámetros distintos que no se pueden (o sería extraordinariamente complejo) estudiar con una sola teoría, es decir, a esa escala son complementarias.
En el presente trabajo se discuten los resultados de simulaciones de los cuatro isómeros del crotonaldehído en fase gaseosa mediante DFT y MD. Se analizan varios observables de interés -energía libre, frecuencias vibracionales, tipo de modo vibracional, absorbancia del modo vibracional, espectro infrarrojo- y se comparan entre sí y con algunos resultados experimentales.
Metodología
Para los cálculos a nivel DFT se usó el método de proyector de ondas aumentadas (PAW) (Blöchl, 1994), como está implementado en el programa VASP (Kresse y Furthmüller, 1996). La energía de intercambio y correlación se calculó con base en la aproximación de gradiente generalizado (GGA) con la parametrización de Perdew-Burke-Ernzerhof (1996). Se estableció el corte de energía cinética para las funciones de onda en 800 eV. En esta teoría se simulan los sistemas a una temperatura de 0 K. Se utilizó una celda cúbica simple de 20 Å de lado para todos los isómeros. Las frecuencias y absorbancias vibracionales se calcularon usando la teoría del funcional de la densidad perturbada (DFPT, por sus siglas en inglés) (Wu et al., 2005). Se calcularon las frecuencias a partir de la matriz Hessiana y las intensidades usando el programa publicado por David Karhánek (2020) basado en la teoría de respuesta lineal.
Para los cálculos con MD se tomaron las estructuras previamente optimizadas vía DFT y se les implementó un potencial híbrido de Lennard-Jones/Coulomb con una transición a 6.0 Å (Plimpton y Thompson, s.f.), como está implementado en el programa LAMMPS (Thompson et al., 2022). Se ajustaron enlaces armónicos a las distancias interatómicas de la estructura de DFT [d(CH) = 1.10 Å, d(C-C) = 1.47 Å, d(C = C) = 1.35 Å, d(C = O) = 1.23 Å] para simular el comportamiento de los dobles enlaces y enlaces sencillos en las moléculas. Se utilizó la misma caja cúbica simple con a = 20 Å. Para la fase de equilibrio se utilizó un termostato tipo Nosé-Hoover con un incremento lineal de la temperatura desde 0 K hasta las temperaturas de 50, 100, 150, 200, 250 y 300 K para la estructura E-(s)-trans y a 300 K para las otras estructuras. Se utilizó un ensamble NVT con un paso temporal de 0.5 fs de 4 ns de duración. Finalmente, se calcularon 8 ns de fase de producción con un ensamble NVT a las temperaturas deseadas, guardando las trayectorias cada 100 fs. Las frecuencias y absorbancias vibracionales se calcularon mediante el método de Kong (2011) y se procesaron usando el programa de Efrem Braun (2016).
Los archivos .data necesarios para correr en LAMMPS fueron generados usando un generador de estructuras para LAMMPS (Haley, 2016). Las imágenes de crotonaldehídos y gráficas en este reporte fueron generadas usando VESTA (Momma y Izumi, 2011) y matplotlib (Hunter, 2007), respectivamente.
Resultados y discusiones
En la Tabla 1 se muestra una comparación de las energías libres relativas calculadas para los cuatro isómeros del crotonaldehído y algunos valores de la literatura. Se observa que la estructura E-(s)-trans es la más estable tanto experimentalmente como en todos los cálculos. Los valores de energías relativas obtenidos mediante DFT en el presente trabajo son razonablemente parecidos a los reportados por Haubrich et al. (2009), en el cual también se realizaron cálculos utilizando DFT. A su vez, las energías relativas obtenidas mediante esta teoría para el isómero E-(s)-cis son bastante parecidas a las determinadas experimentalmente por De Groot y Lamb (1957), lo cual demuestra que estos cálculos tienen un alto grado de confiabilidad. Por su parte, los cálculos de MD predicen el mismo orden de estabilidad para los isómeros, pero las energías relativas obtenidas discrepan de los datos reportados a partir de la utilización de otros métodos. A partir de estos resultados obtenidos se aprecia que los cálculos de MD modelan correctamente de manera cualitativa al sistema, pero no son muy exactos en la predicción más detallada de energías o propiedades vibracionales, como se analizará más adelante.
Tabla 1 Energías relativas de los cuatro isómeros del crotonaldehído.
*(Haubrich et al., 2009), **(de Groot y Lamb, 1957),***energía promedio, -no reportado. Fuente: Elaboración de los autores.
ΔE (eV/átomo)
Estructura
Reportado
Reportado
Calculado
Calculado
E-(s)-trans
0.0
0.0
0.0
0.0
E-(s)-cis
0.093
0.084
0.099
0.009
Z-(s)-trans
0.125
-
0.122
0.022
Z-(s)-cis
0.164
-
0.166
0.130
Realizando un análisis basado en la estadística de Boltzmann se pueden estimar las concentraciones de cada isómero con base en sus diferencias energéticas (ver el Apéndice al final del documento). Suponiendo una temperatura y presión estándar (25 ºC, 1 atm) y usando las energías obtenidas por DFT, se predice que el 96.86% de la muestra está en el isómero E-(s)-trans, el 2.14% en el estado E-(s)-cis y el restante 1.00% en los isómeros Z. Estos porcentajes corresponden con lo reportado en estudios anteriores (Haubrich et al., 2009; Lindenmaier et al., 2017).
En la Figura 2 se muestra un espectro IR experimental del crotonaldehído obtenido del reporte de John Wiley y Sons, Inc. (s. f.) usando WebPlotDigitalizer (Rohatgi, s. f.). Aquí se ilustran los modos vibracionales del crotonaldehído, divididos en seis regiones y con seis tipos de modos vibracionales. Entre 3100 y 2700 cm-1 (rojo) se encuentra la región de vibraciones más energéticas: estiramientos ν(C-H) entre carbono e hidrógeno. Entre 1800 y 1500 cm-1 (azul) está la región de estiramientos ν(C = O) y ν(C = C) de dobles enlaces. Esta región tiene la mayor absorbancia, lo cual significa que aquí se da el mayor cambio de momento dipolar con respecto a la distancia de enlace, según la definición de absorbancia en un espectro (IR infrared: interpretation, 2013). Entre 1460 y 1250 cm-1 (verde) está la región de deformación dentro del plano δ(CH) y el modo de paraguas u(CH3). Entre 1100 y 1200 cm-1 (naranja) está el modo de estiramiento ν(C-C), mientras que entre 1050 y 700 cm-1 (morado) están modos de deformación fuera del plano γ(CH). Finalmente, en frecuencias menores a 650 cm-1 (dorado) están los modos de tijereteo δ(OCC) y deformación δ(CCC), todos característicos del esqueleto de carbonos en la molécula. Estos modos asemejan mucho su comportamiento a los reportados en la literatura (Haubrich et al., 2009; De Groot y Lamb, 1957) y difieren en su posición por no más de 10 cm-1. Un estudio a detalle de estos modos vibracionales fue reportado por Lindenmaier et al. (2017).
Figura 2 Espectro IR experimental del crotonaldehído (absorbancia vs. frecuencia de onda).
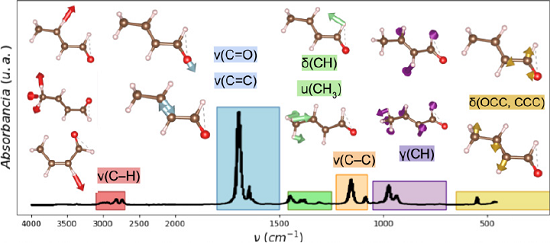
Nota: Los movimientos vibracionales representados son: estiramiento (ν), deformación en el plano [δ(XY)], deformación fuera del plano (γ) y deformación/tijereteo de la cadena de carbonos [δ(XYZ)]. El modo u(CH3) es un modo especial denotado como paraguas (umbrella). Los colores rojo, azul, verde, naranja, morado y dorado representan las regiones de vibración características del crotonaldehído y se encuentran explicados en el texto.
Fuente: John Wiley y Sons, Inc. (s. f.).
En la Figura 3 se muestra una comparación del mismo espectro IR experimental con los espectros obtenidos por DFT para los cuatro isómeros. Se aprecia que el espectro del isómero E-(s)-trans es el que se ajusta de mejor manera con el experimental. También se aprecia cómo los isómeros trans tienen en común los dos picos de mayor absorbancia pertenecientes a la región ν(C = X). El pico ubicado en ~1700 cm-1 (enlace C = O) tiene mayor absorbancia que el ubicado en ~1650 cm-1 (enlace C = C), caso contrario a los isómeros cis. Los isómeros cis presentan una absorbancia casi nula en el modo ν(C-C). Cabe resaltar que la estructura E-(s)-trans presenta picos de absorbancia con las mismas frecuencias que la región γ(CH). Incluso, es el único isómero que presenta el pico de absorbancia en la región δ(XCC) alrededor de 530 cm-1. La ausencia de picos experimentales donde los demás isómeros sí los presentan es indicativo de que estos se encuentran en bajas concentraciones, puesto que el espectro experimental es una suma de las absorbancias de todas las moléculas presentes en la muestra analizada.
Figura 3 Comparación del espectro experimental (negro) del crotonaldehído.

Nota: Con los espectros obtenidos mediante DFT para los isómeros E-(s)-trans (azul), E-(s)-cis (rojo), Z-(s)-trans (verde) y Z-(s)-cis (amarillo).
Fuente: John Wiley y Sons, Inc. (s. f.).
Estos resultados confirman lo encontrado en la Tabla 1, secundando que el isómero E-(s)-trans es el que se encuentra en mayor cantidad. Asimismo, de la comparación de estos espectros se puede intuir cualitativamente la presencia de los otros isómeros. Por ejemplo, el espectro experimental muestra un pico de absorbancia en 2817 y otro en 2735 cm-1. El segundo se atribuye a la estructura E-(s)-trans, pero el primero pertenece seguramente al segundo isómero más estable: E-(s)-cis. Existen modos con absorbancias muy bajas debajo de 500 cm-11 que parecen modelar distintos movimientos de la cadena de carbonos, pero no es posible discutir a detalle debido a la dificultad en medir esta región del espectro experimentalmente.
La Figura 4 ilustra la comparación del espectro IR experimental con los espectros obtenidos por MD para los cuatro isómeros. Estos espectros tienen claras diferencias que se derivan de la representación de los distintos enlaces por el método de MD. Alrededor de 3900 cm-1 se encuentra un modo vibracional de altísima absorbancia. Este modo no corresponde con ninguno de los reportados en los cálculos de DFT ni el experimental. Los modos en este rango de energía se pueden asociar con un estiramiento de un heteroátomo con hidrógeno ν(X-H). En este caso la única posibilidad es un modo ν(O-H), pero incluso, este modo vibracional se ha encontrado experimentalmente debajo de los 3500 cm-1 (Smith, s. f.).
Figura 4 Comparación del espectro experimental (negro) del crotonaldehído.
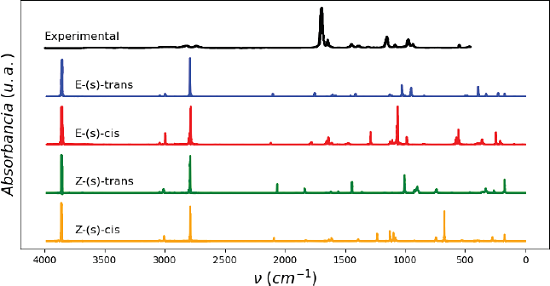
Nota: Con los espectros obtenidos mediante MD (300 K) para los isómeros E-(s)-trans (azul), E-(s)-cis (rojo), Z-(s)-trans (verde) y Z-(s)-cis (amarillo).
Fuente: De Groot y Lamb (1957).
Los dos isómeros E y el Z-(s)-trans son los únicos que presentan absorbancia en la región de estiramiento ν(C = X), aunque que presentan intensidades demasiado bajas. En todos los isómeros los modos vibracionales ubicados en 2700-2800 cm-1 presentan una absorbancia mucho mayor a la experimental, los cuales se asocian con vibraciones de los hidrógenos a las orillas de las moléculas (CH3 o CHO). Por otro lado, los otros modos de estiramiento ν(C-C) tienen una absorbancia muy baja en los isómeros - trans y se ven mejor representados por los isómeros -cis, algo que contradice los resultados de DFT. Es evidente que esta teoría tiene problemas para modelar los modos de estiramiento y que depende mucho del potencial de interacción para una descripción más acertada de los resultados experimentales. Los modos de vibraciones distintos al estiramiento y de energías menores a 1200 cm-1 se asemejan razonablemente bien al espectro experimental. De nuevo, el isómero E-(s)-trans coincide en mayor medida con las frecuencias y absorbancias de los modos de deformación dentro y fuera del plano [δ(CH) y γ(CH)] del espectro.
También se ilustra la comparación del efecto de la temperatura en el cálculo del espectro IR del isómero más estable. Está reportado que conforme desciende la temperatura, las bandas de absorbancia se van afilando y aumenta su intensidad (Cataldo et al., 2010). Esto se puede explicar desde el punto de vista termodinámico considerando que el número de microestados disponibles del sistema disminuye, lo que hace que cada vez más moléculas vibren precisamente a la misma frecuencia, acumulando la misma área bajo la curva en un dominio más pequeño. En particular, aplicando de nuevo la estadística de Boltzmann, se estima que el porcentaje del isómero E-(s)-trans pasa a ser 98.56, 99.57 y 99.94% a temperaturas de 250, 200, 150 K, respectivamente. Debajo de 100 K el porcentaje de este isómero es superior al 99.99%. En otras palabras, a baja temperatura el espectro infrarrojo se resuelve mejor hacia el isómero E-(s)-trans. Estos efectos se observan en la Figura 5, donde hay una reducción gradual en la anchura de los picos de absorbancia. A 50 K estos son casi funciones delta, muy similares a los espectros de DFT. Asimismo, si bien las absorbancias no parecen cambiar para modos de alta energía, el modo que está a 3000 cm-1 y aquellos por debajo de 2000 cm-1 manifiestan también un claro incremento en absorbancia.
Figura 5 Comparación de los espectros calculados mediante MD.

Nota: Con los espectros calculados mediante MD para el isómero más estable (E-(s)-trans) a 300 (rojo), 250 (naranja), 200, (amarillo), 150 (verde menta), 100 (azul claro) y 50 K (azul oscuro).
Fuente: John Wiley y Sons, Inc. (s. f.).
Lindenmaier et al. (2017) midieron experimentalmente este efecto a temperaturas cercanas a la temperatura ambiente (278, 298 y 323 K) y no se reportaron cambios significativos para la mayoría de los modos vibracionales, salvo para uno que está ubicado alrededor de 730.90 cm−1. Este modo se atribuyó al isómero E-(s)-cis y aumenta su intensidad con la temperatura, debido a que este isómero aumenta su concentración. Las temperaturas evaluadas están todas muy cerca entre sí, por lo que no se pueden apreciar los efectos discutidos en los cálculos de MD.
Finalmente, vale la pena reiterar las diferencias prácticas en el uso de ambas teorías. Con los parámetros descritos en la sección de metodología y usando 4 procesadores en paralelo, cada cálculo de MD tomó alrededor de un tercio de hora, mientras que los de DFT tomaron alrededor de 32 hrs cada uno. Queda claro que, si bien DFT predice con mayor precisión las propiedades vibracionales, un cálculo mediante MD arroja resultados cualitativamente aceptables y es mucho más rápido. Esto sin mencionar que la implementación de cálculos a temperaturas finitas a nivel DFT sigue siendo un tema de investigación a nivel teórico (Pittalis et al., 2011; Pribram-Jones, Grabowski y Burke, 2016), mientras que esto viene implícitamente integrado en cálculos por MD. La precisión de los cálculos de MD es totalmente dependiente del campo de fuerza escogido. En particular, Van Duin et al. (2001) describieron el campo de fuerza tipo ReaxFF, que busca describir los distintos órdenes de enlace con mayor precisión, por lo que su uso podría aumentar la precisión de los resultados obtenidos mediante cálculos de MD. Hay varios tipos de definición de este potencial y todos requieren de la optimización de una gran cantidad de parámetros -movimientos de enlaces y ángulos, energías de activación y reacción, ecuaciones de estado, energías de superficie, entre otros- (Software for Chemistry & Materials, 2021), lo que aumenta su costo computacional. Esto hace que el uso de estos potenciales sea poco común y el encontrar (o crear) un potencial de este tipo optimizado para estudiar propiedades vibracionales sea una tarea que posiblemente consuma mucho más tiempo del que pretende ahorrar. En la práctica, resulta más conveniente realizar un cálculo mediante DFT para obtener resultados más precisos.
Conclusiones
Se calcularon las propiedades energéticas y vibracionales del crotonaldehído usando dos programas con niveles de teoría distintos. Ambas teorías predicen el orden correcto de estabilidad en los isómeros, pero los cálculos de DFT coinciden de mejor forma con reportes experimentales. Mediante un análisis de las energías basado en la estadística de Boltzmann, se estimó que el isómero E-(s)-trans presenta una concentración de 96.86% en la muestra a presión y temperatura estándar. Los espectros IR obtenidos mediante ambas teorías muestran que el isómero E-(s)-trans es el que se adecua más a los datos experimentales. Se puede determinar cualitativamente la presencia de otros isómeros por la posición de los picos de absorbancia. Por otra parte, los espectros calculados mediante MD describen con mayor precisión la región de baja energía del espectro (<1500 cm-1), fallando particularmente en describir los modos de estiramiento de los isómeros. Se describió el efecto de la temperatura en el espectro IR del isómero E-(s)-trans usando MD. Se observó el afilamiento de los espectros conforme disminuye la temperatura (como está reportado experimentalmente) y se explicó este fenómeno usando la misma estadística de Boltzmann. Los errores presentes en los cálculos de MD se atribuyen a la dificultad para describir los distintos tipos de enlace en el crotonaldehído. Se comprobó la gran precisión y exactitud presente en DFT a comparación de MD en este sistema. Se pueden escoger campos de fuerza más detallados para aumentar la precisión de los cálculos de MD, pero como regla general DFT es más preciso que MD y su costo computacional aumenta en mayor medida conforme aumenta el número de átomos en el sistema. Hay que considerar el número de átomos en el sistema, los parámetros de interés, la precisión deseada y los recursos computacionales disponibles para escoger el nivel de teoría a utilizar en los cálculos.
Referencias
- ATSDR. (s. f.). Toxfaqs™-Letter a | toxic substance portal | atsdr. (Consultado, noviembre 1, 2021). https://wwwn.cdc.gov/TSP/ToxFAQs/ToxFAQsLanding.aspx
- Bhoskar, Ms. T., Kulkarni, Mr. O. K., Kulkarni, Mr. N. K., Patekar, Ms. S. L., Kakandikar, G. M. y Nandedkar, V. M. (2015). Genetic algorithm and its applications to mechanical engineering: A review. Materials Today: Proceedings, 2(4-5): 2624-2630. https://doi.org/10.1016/j.matpr.2015.07.219
- Blöchl, P. E. (1994). Projector augmented-wave method. Physical Review B, 50(24): 17953-17979. https://doi.org/10.1103/PhysRevB.50.17953
- Braun, E. (2016). Open source code: Calculating an ir spectra from a lammps simulation. Zenodo. https://doi.org/10.5281/ZENODO.154672
- Car, R. y Parrinello, M. (1985). Unified approach for molecular dynamics and density-functional theory. Physical Review Letters, 55(22): 2471-2474. https://doi.org/10.1103/PhysRevLett.55.2471
- Cataldo, F., Iglesias-Groth, S. y Manchado, A. (2010). Low and high temperature infrared spectroscopy of c 60 and c 70 fullerenes. Fullerenes, Nanotubes and Carbon Nanostructures, 18(3): 224-235. https://doi.org/10.1080/15363831003782940
- De Groot, M. S. y Lamb, J. (1957). Ultrasonic relaxation in the study of rotational isomers. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 242(1228): 36-56. https://doi.org/10.1098/rspa.1957.0152
- Gallezot, P. y Richard, D. (1998). Selective hydrogenation of α,β-unsaturated aldehydes. Catalysis Reviews, 40(1-2): 81-126. https://doi.org/10.1080/01614949808007106
- Haley, B. (2016). LAMMPS structure generator. https://doi.org/https://doi.org/10.4231/D34B2X60F
- Haubrich, J., Loffreda, D., Delbecq, F., Sautet, P., Krupski, A., Becker, C. y Wandelt, K. (2009). Adsorption of α,β-unsaturated aldehydes on pt(111) and pt−sn alloys: Ii. crotonaldehyde. The Journal of Physical Chemistry C, 113(31): 13947-13967. https://doi.org/10.1021/jp903473m
- Honorio, T. (2019). Monte Carlo molecular modeling of temperature and pressure effects on the interactions between crystalline calcium silicate hydrate layers. Langmuir, 35(11): 3907-3916. https://doi.org/10.1021/acs.langmuir.8b04156
- Hunter, J. D. (2007). Matplotlib: A 2d graphics environment. Computing in Science y Engineering, 9(3): 90-95. https://doi.org/10.1109/MCSE.2007.55
- Infrared: Interpretation. (2013, octubre 2). Chemistry LibreTexts. https://chem.libre-texts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Spectroscopy/Vibrational_Spectroscopy/Infrared_Spectroscopy/Infrared%3A_Interpretation
- Karhánek, D. (2020). Dakarhanek/vasp-infrared-intensities: Vasp-infrared-intensities (v1.0) [Computer software]. Zenodo. https://doi.org/10.5281/ZENODO.3930989
- Kong, L. T. (2011). Phonon dispersion measured directly from molecular dynamics simulations. Computer Physics Communications, 182(10): 2201-2207. https://doi.org/10.1016/j.cpc.2011.04.019
- Kresse, G. y Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Physical Review B, 54(16): 11169-11186. https://doi.org/10.1103/PhysRevB.54.11169
- Leach, A. R. (2001). Molecular modelling: Principles and applications, Chapter 4: Empirical Force Field Models: Molecular Mechanics, 2a ed. Prentice Hall, 165-247.
- Lee, J. W., Nilson, R. H., Templeton, J. A., Griffiths, S. K., Kung, A. y Wong, B. M. (2012). Comparison of molecular dynamics with classical density functional and Poisson-Boltzmann theories of the electric double layer in nanochannels. Journal of Chemical Theory and Computation, 8(6): 2012-2022. https://doi.org/10.1021/ct3001156
- Lindenmaier, R., Williams, S. D., Sams, R. L. y Johnson, T. J. (2017). Quantitative infrared absorption spectra and vibrational assignments of crotonaldehyde and methyl vinyl ketone using gas-phase mid-infrared, far-infrared, and liquid raman spectra: S-cis vs s-trans composition confirmed via temperature studies and ab initio methods. The Journal of Physical Chemistry A, 121(6): 1195-1212. https://doi.org/10.1021/acs.jpca.6b10872
- Magnasco, V. (2013). Post-hartree-fock methods. En Elementary molecular quantum mechanics. Elsevier, 681-722. https://doi.org/10.1016/B978-0-444-62647-9.00016-6
- Momma, K. y Izumi, F. (2011). Vesta 3 for three-dimensional visualization of crystal, volumetric and morphology data. Journal of Applied Crystallography, 44(6): 1272-1276. https://doi.org/10.1107/S0021889811038970
- Oukhrib, R., Abdellaoui, Y., Berisha, A., Abou Oualid, H., Halili, J., Jusufi, K., Ait El Had, M., Bourzi, H., El Issami, S., Asmary, F. A., Parmar, V. S. y Len, C. (2021). DFT, Monte Carlo and molecular dynamics simulations for the prediction of corrosion inhibition efficiency of novel pyrazolylnucleosides on Cu(111) surface in acidic media. Scientific Reports, 11(1): 3771. https://doi.org/10.1038/s41598-021-82927-5
- Perdew, J. P., Burke, K. y Ernzerhof, M. (1996). Generalized gradient approximation made simple. Physical Review Letters, 77(18): 3865-3868. https://doi.org/10.1103/PhysRevLett.77.3865
- Pittalis, S., Proetto, C. R., Floris, A., Sanna, A., Bersier, C., Burke, K. y Gross, E. K. U. (2011). Exact conditions in finite-temperature density-functional theory. Physical Review Letters, 107(16): 163001. https://doi.org/10.1103/PhysRev-Lett.107.163001
- Plimpton, S. J. y Thompson, A. P. (s.f.). Pair_style lj/cut/coul/cut command-Lammps documentation. Retrieved November 1, 2021, from
https://docs.lammps.org/pair_lj_cut_coul.html - Pribram-Jones, A., Grabowski, P. E. y Burke, K. (2016). Thermal density functional theory: Time-dependent linear response and approximate functionals from the fluctuation-dissipation theorem. Physical Review Letters, 116(23): 233001. https://doi.org/10.1103/PhysRevLett.116.233001
- PubChem. (s. f.-a). Crotonaldehyde. (Consultado, noviembre 1, 2021). https://pub-chem.ncbi.nlm.nih.gov/compound/447466
- PubChem. (s. f.-b). Hazardous substances data bank (Hsdb): 2871. (Consultado, noviembre 1, 2021). https://pubchem.ncbi.nlm.nih.gov/source/hsdb/2871#section=Human-Health-Effects
- Qin, W., Li, X., Bian, W.-W., Fan, X.-J. y Qi, J.-Y. (2010). Density functional theory calculations and molecular dynamics simulations of the adsorption of biomolecules on graphene surfaces. Biomaterials, 31(5): 1007-1016. https://doi.org/10.1016/j.biomaterials.2009.10.013
- Rogge, S. M. J., Goeminne, R., Demuynck, R., Gutiérrez‐Sevillano, J. J., Vandenbrande, S., Vanduyfhuys, L., Waroquier, M., Verstraelen, T. y Van Speybroeck, V. (2019). Modeling gas adsorption in flexible metal-organic frameworks via hybrid monte carlo/molecular dynamics schemes. Advanced Theory and Simulations, 2(4): 1800177. https://doi.org/10.1002/adts.201800177
- Rohatgi, A. (s. f.). Webplotdigitizer. (Consultado, noviembre 1, 2021). https://automeris.io/WebPlotDigitizer/
- Smith, B. (s. f.). Alcohols-The rest of the story. Spectroscopy Online. (Consultado, noviembre 1, 2021). https://www.spectroscopyonline.com/view/alcohols-rest-story-alf3
- Software for Chemistry y Materials. (2021). ReaxFF - Force field format specification. https://www.scm.com/doc/ReaxFF/ffield_descrp.html
- Thompson, A. P., Aktulga, H. M., Berger, R., Bolintineanu, D. S., Brown, W. M., Crozier, P. S., in ’t Veld, P. J., Kohlmeyer, A., Moore, S. G., Nguyen, T. D., Shan, R., Stevens, M. J., Tranchida, J., Trott, C. y Plimpton, S. J. (2022). LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Computer Physics Communications, 271: 108171. https://doi.org/10.1016/j.cpc.2021.108171
- Van Duin, A. C. T., Dasgupta, S., Lorant, F. y Goddard, W. A. (2001). ReaxFF: A reactive force field for hydrocarbons. The Journal of Physical Chemistry A, 105(41): 9396-9409. https://doi.org/10.1021/jp004368u
- Wiley, J. y Sons, Inc. (s.f.). Crotonaldehyde-Ftir-Spectrum-Spectrabase. (Consultado, noviembre 1, 2021). https://spectrabase.com/spectrum/69ZANaBjwub
- Wu, X., Vanderbilt, D. y Hamann, D. R. (2005). Systematic treatment of displacements, strains, and electric fields in density-functional perturbation theory. Physical Review B, 72(3): 035105. https://doi.org/10.1103/PhysRevB.72.035105
- Zhang, L., Zhou, M., Wang, A. y Zhang, T. (2020). Selective hydrogenation over supported metal catalysts: From nanoparticles to single atoms. Chemical Reviews, 120(2): 683-733. https://doi.org/10.1021/acs.chemrev.9b00230
Apéndice
Cálculo de las concentraciones de los isómeros
El presente análisis está basado en el trabajo publicado por Lindenmaier et al. (2017). Se parte de considerar a todos los isómeros como estados no-degenerados, con el isómero de menor energía (E-(s)-trans) ubicado en el cero de energía y las energías del resto tomadas relativas a este. Una vez definido esto se aplicará la estadística de Boltzmann basada en las energías moleculares. El número total de moles es:
donde los subíndices 1, 2, 3 y 4 hacen referencia a los isómeros E-(s)-trans, E-(s)-cis, Z-(s)-trans y Z-(s)-cis, respectivamente. Dicho esto, se puede expresar el número de moles de cada isómero (nx , x = 1, 2, 3, 4) en términos de una distribución de Boltzmann como sigue:
donde Ex ,(x = 1, 2, 3, 4) es la energía relativa de cada isómero (dadas en la Tabla 1), z es la función de partición, R es la constante de gases (8.314 J mol-1 K-1) y T la temperatura (K). Recordando que la energía relativa del isómero E-(s)-trans se define como el cero (E1 = 0), la ecuación A.2 se reduce a:
Al dividir las expresiones A.3-6 entre n se obtienen las fracciones molares de los isómeros (X1, X2, X3, X4), las cuales suman a uno. Efectuando esta suma y despejando la función de partición se obtiene:
Finalmente, una vez que se conoce la expresión de la función de partición se sustituye su valor en las expresiones A.3-6 y se divide entre n para encontrar las expresiones de las fracciones molares (concentraciones) de los isómeros:
◊ Nuestro agradecimiento a los proyectos DGAPA-UNAM IN105722 e IA100822 y al proyecto CONACyT A1-S-9070 por su apoyo parcial al desarrollo de este proyecto. Los cálculos se llevaron a cabo en el centro de supercómputo DGCTIC-UNAM LANCAD-UNAM-DGTIC-368 y LANCAD-UNAM-DGTIC-051. J.G.S. Se agradece al Laboratorio Nacional de Supercómputo del Sureste de México y al Centro de Supercómputo THUBAT KAAL IPICYT. J.G.S. Al profesor Aníbal Muñoz por todos los buenos momentos, las pláticas constructivas, y por siempre estimular un ambiente de superación académica. Agradecemos también a A. Rodríguez Guerrero y a Alejandro David Ruvalcaba Briones por el apoyo técnico.