www.mundonano.unam.mx | Mundo Nano
http://dx.doi.org/10.22201/ceiich.24485691e.2022.29.69700 | 15(29), 1e-21e, julio–diciembre 2022
Research articles
Au-Ru nanoparticles in catalysis, analysis from first-principles calculations◊
Nanopartículas Au-Ru en catálisis, análisis a partir de cálculos a primeros principios
Uriel Molina*
Rodrigo Mojica**
Ana E. Torres*♦
* Universidad Nacional Autónoma de México, Instituto de Ciencias Aplicadas y Tecnología.
** Instituto Politécnico Nacional, Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada.
♦ Correspondence author: ana.torres@icat.unam.mx
Abstract:
Nobel-metal based bimetallic nanoparticles (BNPs) are composed of two different metals presenting heteroatom interactions. In these nanomaterials it is possible to tune the relative composition that allows for the modulation of electronic and catalytic properties. They are of great interest for their technological and industrial applications due to their catalytic properties which may exceed those of their monometallic analogue structures. A theoretical perspective on the electronic, stability and reactivity related properties of gold, ruthenium and Au-Ru nanoparticles is presented herein. This analysis considered the use of first-principles methods and the cluster approach to get a physical insight into the novel properties that arise from the combination of two metals in the nano and sub-nano scale. Au-Ru BNPs may present a higher catalytic efficiency than the monometallic structures due to the synergy between the metals in the CO oxidation reaction. However, the effect of Ru over the Au-based NPs on their enhanced catalytic activity is not well understood. A density functional theory (DFT) study of one Au-Ru cluster model was performed to analyze its electronic properties and to gain a better understanding in the stability of structures with various metal compositions.
Based on the computed mixing enthalpy, the Au-Ru cluster with a core-shell type morphology and a relative composition close to 1:0.75 was determined as the most stable one. Finally, a CO oxidation reaction pathway different from that determined for Au-NPs was presented for the free particle occurring in the Au-Ru interface. O2 may undergo adsorption on a Ru site through a dissociative process. The computed CO oxidation barrier height is lower than that found for the monometallic Ru clusters but is higher than that determined for Au clusters. This study will guide further research on this kind of model nanostructures in heterogeneous catalysis.
Keywords: bimetallic, nanoparticles, DFT, oxidation, catalysis.
Resumen:
Las nanopartículas bimetálicas (BNPs) basadas en metales nobles están compuestas por dos diferentes metales que presentan interacciones entre heteroátomos. En estos nanomateriales es posible regular su composición relativa lo cual permite modular las propiedades electrónicas y catalíticas. Son de gran interés por sus aplicaciones tecnológicas y en la industria debido a sus propiedades catalíticas que pueden ser superiores a las de estructuras análogas monometálicas. En este trabajo se presenta una perspectiva teórica de las propiedades electrónicas, estabilidad y propiedades relacionadas con reactividad de nanopartículas de oro, rutenio y Au-Ru. En este análisis se consideró el uso de métodos basados en primeros principios y en la aproximación de clúster para adquirir una comprensión física de las nuevas propiedades que surgen de la combinación de dos metales en la escala nano y sub-nano. Las BNP-s Au-Ru pueden presentar una mayor actividad catalítica en la reacción de oxidación de CO que las estructuras monometálicas debido a la sinergia entre los metales. Sin embargo, hasta el momento se desconoce el efecto del Ru sobre las propiedades de las NPs de Au que podrían explicar la mayor actividad catalítica. Se realizó un estudio DFT para un modelo de clúster Au-Ru con la finalidad de analizar las propiedades electrónicas y para obtener una mejor comprensión de la tendencia en estabilidad de las estructuras cuando se varía la composición. Con base en las entalpías de mezclado calculadas, el clúster Au-Ru de morfología tipo core-shell y con una composición relativa cercana a 1:0.75 se determinó como más estable. Finalmente, se presentó una trayectoria de reacción para la oxidación de CO en la partícula libre, distinta de aquella determinada para nanopartículas de oro, que ocurre en la interfase Au-Ru. La molécula de O2 puede sufrir una adsorción disociativa en un sitio de Ru. La altura de la barrera de oxidación de CO es menor que aquella encontrada para cúmulos monometálicos de rutenio, pero es más alta que aquella determinada para cúmulos de oro. Los resultados del presente trabajo servirán de guía en estudios posteriores para este tipo de nanoestructuras modelo en catálisis heterogénea.
Palabras clave: bimetálico, nanopartículas, DFT, oxidación, catálisis.
Received: September 12, 2021
Accepted: December 17, 2021.
Introduction
The term nanoparticle refers to objects with a diameter between 1 and 100 nm, and particle refers to an object that may be crystalline (a nanocrystal), amorphous or have a non-crystalline ordered structure (a cluster, such as a fullerene). Nanoparticles composed of two different metals present novel physical and catalytic properties. The bimetallic nanoparticles (BNPs) exhibit the properties of each constituting metal and new properties arising from the synergy of both metals. Among their interesting applications in the industry is found their use as catalysts for hydrocarbon conversion to obtain high octane fuel in industrial reforming (An and Somorjai, 2015).
The morphology of the BNP can vary from alloy to core-shell and can be mediated by the preparation method as well as the conditions and it is highly influenced by each metal properties (Nasrabadi et al., 2016; Zaleska-Medynska et al., 2016). The alloying or segregation of the two metals in a BNP is affected by the relative strengths of metal-metal bonds, the surface energies of the bulk elements, the difference in the standard reduction potentials of the used metals and the relative atomic sizes (Ferrando et al., 2008; Tojo et al., 2017; Yao et al., 2021). The higher strengths of heteronuclear (M1-M2) over homonuclear (M1-M1, M2-M2) bonds tend to favor the mixing of metals. Otherwise, the segregation may occur thus inducing that the metal with stronger M-M bond conform the core of the NP. For instance, the DFT computed dissociation energies are 2.38 eV for Ru-Ru, 2.05 eV for Au-Au and 2.04 eV for Ru-Au bond attesting the preference of ruthenium to interact through homonuclear bonding with tendency to form the core of BNP (Garbounis et al., 2010). In the same line, the metal with lower surface energy tends to locate in the surface of the NP and smaller atoms tend to occupy the core. The reported surface energy for Au is 1.506 J/m2 whereas for Ru is 3.043 J/m2, then when both metals are mixed gold will migrate to the BNP surface (Zaleska-Medynska et al., 2016). The mixing of metals in alloys explained through the Miedema’s model (Miedema et al., 1973) is favored by the electron transfer due to a difference in the electronegativity of the constituent elements which corresponds to a mechanism equalizing the electrochemical potential throughout the crystal. Then the greater electronegativity of gold (Au 2.54) compared to that of ruthenium (Ru 2.2) might induce electron transfer from Au to Ru. In case of supported BNPs the binding strength to surface ligands or atoms affects the final structure of BNPs.
The reduction potential of the metal ions is an important factor that may affect the BNP morphology. The metal ions are more prone to be reduced if they exhibit a higher reduction potential. It is known that a large difference in the reduction potential between the metals in a BNP leads to core- shell morphology while similar reduction potentials tend to form an alloy structure (Bhol et al., 2020). The standard redox potentials of gold and ruthenium vary significantly (E0Au3+/Au0 = 1.50 V, E00Ru3+/Ru0 0.60 V) that if BNPs are prepared under reducing conditions gold will be reduced firstly and it will render higher composition in the nanostructure.
Bimetallic nanoparticles have been employed as catalysts in heterogeneous phase free or supported in metal-oxides. It has been observed that BNPs can show higher catalytic activity compared to their monometallic analogue structures with improved efficiency or selectivity in a catalytic reaction (Dimitratos et al., 2012; Prati et al., 2018). The catalytic activity enhancement in BNPs can be ascribed to the small diameter of BNPs, the electron transfer between the metals composing the BNPs structures and the modification of electronic properties (Zaleska-Medynska et al., 2016).
Recently, Zanella et al. reported a preparation method of gold-based bimetallic catalysts supported on TiO2 conducted by the sequential deposition-precipitation with urea to study the catalytic oxidation of CO (Calzada et al., 2017, 2020). They reported higher catalytic activity for Au-Ru/TiO2 in CO oxidation compared to the monometallic counterparts (Calzada et al., 2020). Particularly, the CO oxidation is considered a model reaction in heterogeneous catalysis used to probe the catalytic activity of novel materials (Freund et al., 2011).
Gold nanoparticles smaller than 5 nm are effective catalysts for low temperature CO oxidation. Even more, it has been proposed that CO oxidation in a gold NP surface proceeds through a Langmuir-Hinshelwood mechanism through the dissociative adsorption of O2 (Louis, 2007). However, for CO oxidation in small Au clusters, it has been proposed the formation of the adsorbed OCOO* intermediate which may be responsible for the low temperature catalytic activity of gold due to the reactivity of this peroxide species (Landman et al., 2007). In a theoretical study of the first CO oxidation step catalyzed by gold clusters, it was found that the O-O bond scission of the OCOO* intermediate as the rate limiting step of the CO oxidation reaction. The reported activation energies for the O-O bond scission barrier for octahedral NP model structures are around 0.2e V (Liu et al., 2018). The product of this reaction step is a CO2 free molecule.
Unlike gold, for ruthenium clusters it has been found atomic oxygen adsorbed on the Ru surface sites. Ab initio calculations at PBE-DNP (a double numerical basis sets plus polarization function and an effective core potential for ruthenium) level of theory on the CO oxidation of bare Ru10 clusters revealed a transition state with a different configuration compared to that found for Au clusters (Zhang et al., 2014). Indeed, no OCOO* intermediate was found along the reaction pathway. The CO approached the adsorbed oxygen atom toward the CO2 formation. The CO oxidation barrier of 1.1 eV (25.4 kcal/mol) was reported for the neutral Ru cluster and evolved to a stable CO2 adsorbed product.
As aforementioned, bimetallic Au-Ru NPs supported over a reducible oxide have been synthesized and exhibited higher catalytic activity in the CO oxidation reaction than gold NPs (Calzada et al., 2020). However, the origin of this synergic effect induced by the ruthenium incorporation in the bimetallic nanoparticle still remains unknown. To our knowledge, the electronic properties and possible reaction mechanism of these novel catalytic materials have not yet been reported. Then to analyze the effect of ruthenium on the electronic properties and reactivity for CO oxidation, in gold-based bimetallic nanoparticles, it was conducted a first-principles study on bimetallic Au-Ru clusters. The results presented herein aim at guiding a further study on the supported structures.
Theoretical methods
The calculations were performed using the DFT-GGA approximation, with the exchange-correlation functional PBEsol (Perdew et al., 2008) within the projector augmented wave (PAW) method (Blöchl, 1994; Kresse G., Joubert, 1999). This technique spans reciprocal space with a plane-wave basis set. The D3 (BJ) Grimme dispersion correction was used in the calculations (Grimme et al., 2010, 2011). A plane-wave basis set was used with a kinetic cutoff energy of 400 eV. An electronic smearing method was incorporated to carry out the DFT calculations, and a 0.01 eV/Å force tolerance was considered on each atom. The Gamma-point only sampling was used for the Brillouin zone integration. QuantumATK (NanoLab,v R-2020.09) (Stradi et al., 2017) and Vesta (Momma y Izumi, 2011) software packages were used for the visualization of the structural models.
The geometry of the system has been relaxed, and the atom centered in the BNP model structure was fixed to avoid forces convergence oscillations. PAW standard potentials were employed, as implemented in the Vienna Ab initio Simulation Package (VASP version 5.4.4 ) (Kresse and Furthmüller, 1996a, 1996b; Kresse y Hafner, 1993, 1994). As a first approach the cuboctahedral bimetallic cluster models were optimized in a periodic supercell with vacuum and a lattice parameter of 20 Å. The O2 (in its triplet state) and CO adsorption were explored through the abovementioned approach. Likewise, cohesive energies and formation enthalpies were computed. This was followed by a theoretical study of the CO oxidation mechanism in the Au-Ru interface of an Au-Ru bimetallic particle model with relative composition 1:0.75 at PBE-D3(BJ)/LANL2DZ level of theory with the software Gaussian 16 (Frisch et al., 2016). The electronic ground state of the cluster was explored. Truncated cuboctahedron has shown to be the preferred geometry for gold nanoparticles and is taken as reference to study bimetallic clusters (Pundlik et al., 2011).
The cuboctahedron model was built by following the next procedure presented as a tutorial.
Tutorial to build a truncated cuboctahedral nanoparticle with ASE
ASE is an atomic simulation environment based on python language whose main purpose is setting up and postprocessing atomistic simulations. The minimum requirements for its installation and use are the tools and libraries Python 3.6 (or newer), NumPy, SciPy and Matplotlib, so it is highly recommended to use the latest Anaconda Python distribution. The individual installation and manage of the required libraries/packages are also feasible.
In this tutorial, ASE installation and examples will be explained with the use of Anaconda Python distribution for simplicity.
ASE installation
In a Linux operating system (OS) open a bash terminal and type “$ conda activate” to activate the base conda environment in which are defined the necessary libraries to install ASE. In the case of Windows OS users will open the Anaconda Powershell Prompt and follow the same instructions. Make sure that the minimum requirements are available with “$ conda list” command. If some of them are missing you can use “$ conda install libpack_name” to install any of them. If you have a predefined environment or want to create a new one with the minimum requirements for installation you can use:
$ env_name activate
$ conda create -n new_env_name pythonX.X.X numpy scipy matplotlib (here X.X.X are the numbers of any compatible python version).
Once you have already prepared your working environment, for ASE installation type:
$ conda install -c conda-forge ase
This command will automatically install ASE package through conda. Declaring the environment variables in the user’s $PATH will not be necessary.
Building a nanoparticle with ASE
In any conda-based environment ASE simply works with python scripts, so for any task to be developed with ASE, the instructions in the python programming language must be declared in a .py extension file and executed with:
$ python name_task.py
Immediately the program runs if it does not have any syntax error.
ASE contains the general module ase.cluster which is focused on building nanoparticles or atomic clusters for different crystal structures. This module works separately through predefined crystal structure functions, declaring the number of layers and directions or by Wulff constructions. From this module are imported the functions and submodules needed to build nanoparticles with different geometries. It is suggested to revise the options and availability of special functions to build specific nanoparticles in the ase.cluster module description (Larsen et al., 2017).
As an example, the building of cuboctahedral Au nanoparticles with 13 and 55 atoms, from predefined functions is described.
Example 1.13 Au cluster
For the nanoparticle with 13 atoms the octahedron function must be invoked in the ase.cluster.octahedron submodule. Other structural submodules available in the ase.cluster are icosahedral and decahedral, prior to be used their own parameters can be found in each ASE module description. In this case, for a cuboctahedron that can be built from a truncated octahedral, it is required the octahedral function. This function needs at least three parameters: the element symbol (Au), the cutoff value defines the number of layers cut at each vertex of the octahedron and the length which corresponds to the number of atoms on the edges of the regular octahedron ((2 * cutoff )+ 1). To visualize the Au nanoparticle and save its atomic coordinates in a .xyz file, the functions view and write are used from ase.visualize and ase.io modules, respectively.
The octahedron function must be declared with its parameters and assigned to the “atoms” variable. An example of a python script to build a 13 Au cuboctahedral cluster with ASE is presented next:
from ase.cluster.octahedron import octahedron
length = 3
cutoff = 1
atoms = Octahedron(‘Au’, length, cutoff)
from ase.visualize import view
from ase.io import write
write(‘Au_np_13.xyz’, atoms)
write(‘Au_np_13.png’, atoms)
view(atoms)
This script produces two files: the cartesian coordinates file (Au_np_13. xyz) and an image of the nanoparticle (Au_np_13.png) in a .png format. The produced Au cluster must have 13 atoms arranged in a cuboctahedral distribution. Furthermore, the ASE graphical user interface (GUI) displays the Au nanoparticle. With the ASE’s GUI it is also possible to make some modifications to the structure and visualize it from different perspectives. Figure 1 shows the cluster obtained from the script displayed above. The coordinates are presented in the supporting information.
Figure 1 Edges truncation of a) Au19 octahedral cluster produced the b) cuboctahedral Au13 cluster model.
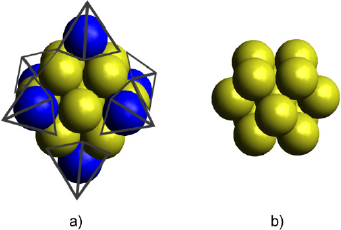
Source: Author’s elaboration.
Example 2. Au 55 cuboctahedral NP
To build a larger Au55 cuboctahedral NP model the parameters that must be changed from the previous script are the length = 5 and cutoff = 2.
The Au55 cuboctahedral nanoparticle model is presented in Figure 2. The coordinates of this cluster are presented in the supporting information.
Figure 2 Truncation of a) Au85 octahedral NP produced the b) cuboctahedral Au55 NP model.
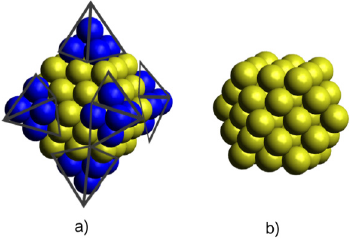
Source: Author’s elaboration.
Calculation of stability properties from first principles calculations for the bimetallic nanoparticle model.
Some of the properties that enable to perform a comparative study of the stability between nanoparticles with the same number of atoms and that can be computed through first principles methods are the cohesive energy and the formation enthalpy. The cohesive energy is the energy required to dissociate the nanoparticle into its constituent neutral free atoms at 0 K. The cohesive energy of a bimetallic nanoparticle is associated with the reaction of the decomposition of the BNP to the noninteracting atoms in the gas phase (Dovesi et al., 2005).
The reaction energy can be computed from:
Given that the reaction needs an input of energy to proceed, the respective reaction energy is positive for a thermodynamic stable crystal. The cohesive energy positive value indicates the thermodynamic stability of the NP. It can be computed trough first principles - based calculations by computing the total energy of the constituent atoms separately and that of the NP structure (Khandy et al., 2019). For a bimetallic NP the cohesive energy is computed as follows:
Where Ecoh is the cohesive energy, EXm Yn is the energy of the bimetallic NP, mEX and nEY are the energies of each separate atom multiplied by the number of each atom (m or n) present in the NP. This property varies with the particle size, thus when a monometallic nanoparticle is large enough the cohesive energy approaches to the cohesive energy of the bulk material. For that reason, when comparing the stability of bimetallic NPs with different geometries, morphology and relative composition, the number of atoms composing the structures must be the same.
Another property calculated herein to analyze the relative stability between different BNPs is the mixing enthalpy which can be computed as the enthalpy difference between the two constituents in a NP pure monometallic state and the mixed state. A negative value indicates a favorable mixing tendency and a greater stability. It can be defined as follows (Lu et al., 2017):
The mixing enthalpy is denoted herein as ΔHf , while the energy of the bimetallic NP (containing x + y metal atoms) corresponds to Exm yn . The energies of the pure clusters composed by each metal (x and y) corresponds to Exm + n and Eym + n and mi and ni are the fractions of each atom present in the NP computed as:
The energies for the pure or mixed NPs were obtained from fully relaxed structures.
Results and discussion
The cuboctahedral Au-Ru bimetallic cluster models containing 13 atoms with core-shell type morphology were built and optimized. The relative composition of gold and ruthenium in the clusters varied as shown in Figure 3 (c-f). The expected composition expressed as Au to Ru ratio is presented in bold, while the real relative compositions given the number of atoms in the structure are displayed between parentheses.
Figure 3 Optimized monometallic a) Au13 and b) Ru13 clusters and bimetallic clusters with relative Au:Ru compositions c) 1:1(1:0.9), d) 1:0.75(1:0.6), e) 1:0.5(1:0.4) and f) 1:0.25(1:0.3).

Color code: Au: yellow and Ru: gray.
Source: Author’s elaboration.
Their relative stability was analyzed by computing the cohesive and mixing energies from first-principles calculations and with equations 3, 4 and 5. The results are presented in Table 1.
Table 1 Cohesive energies and formation enthalpies computed for the monometallic M13 (M = Au, Ru) and bimetallic AunRum (n + m = 13) clusters with core-shell type morphologies.
Source: Author’s elaboration.
Morphology
Composition
Ecoh (eV)
ΔHf(eV)
Core-shell
1:1
3.90
-0.11
Core-shell
1:0.75
3.72
-0.15
Core-shell
1:0.50
3.40
-0.05
Core-shell
1:0.25
3.24
-0.10
Monometallic
1:0
2.50
Monometallic
0:1
5.28
As can be seen for the monometallic structures, the cohesive energy of the pure Ru cuboctahedral cluster is greater than that of the gold one. Then the bimetallic cluster with the most composition of ruthenium presented a greater cohesive energy thus it is interpreted as more stable. From experiments of supported BNPs it is known that the optimal composition Au:Ru ratio that exhibited the best catalytic activity accompanied with a synergic effect is 1:0.75 (Calzada et al., 2020). The mixing enthalpy revealed a stability in agreement with experimental observations (being more negative for the 1.0.75 composition) even in the absence of the support, then this relative amount was considered for further calculations.
Different electronic spin states were computed for the 1:0.75 bimetallic cluster and the results are presented in Table 2.
Table 2 Relative energies in kcal/mol for the Au-Ru bimetallic cluster in quintet, triplet and singlet electronic spin states corresponding to 4, 2 and 0 unpaired electrons, respectively.
Source: Author’s elaboration.
Number of unpaired electrons
4
2
0
Relative energy (kcal/mol)
0.0
3.5
8.0
The highest studied quintet spin multiplicity was detected as the ground state for the bimetallic cluster, then the electronic state of ruthenium atom prevailed (4d75s1, 5F). This cluster is composed by eight gold atoms and five ruthenium atoms, the odd number of ruthenium atoms might be affecting the final spin state of the structure. An even number might lead to electron pairing between the electrons of each Ru atom.
The oxygen molecule adsorption was explored on the Au8Ru5 cluster. The adsorption sites were explored firstly through PAW-PBEsol calculations by approaching O2 to each the surface atoms on the bimetallic cluster from an initial distance of 3.5 Å. The adsorption energies were computed and the configurations that presented a greater adsorption energy (more negative) are presented in Figure 4. The remaining computed structures presented meanin-gless adsorption energies approaching zero.
Figure 4 O2 adsorption energies (in eV) computed at PAW-PBEsol level of theory for different explored adsorption sites.

Color code: Au: yellow, Ru: gray and O: red.
Source: Author’s elaboration.
The most stable structure (a in Figure 4) resulted in a dissociated oxygen molecule, this dissociation proceeds barrierless. This structure (a in Figure 4) was re-optimized at PBE-D3(BJ)-LANL2DZ level of theory and used to perform the study of O2 adsorption (Figure 5) and CO oxidation mechanism.
Figure 5 O2 adsorption energies (in eV) computed at PAW-PBEsol level of theory for different explored adsorption sites.
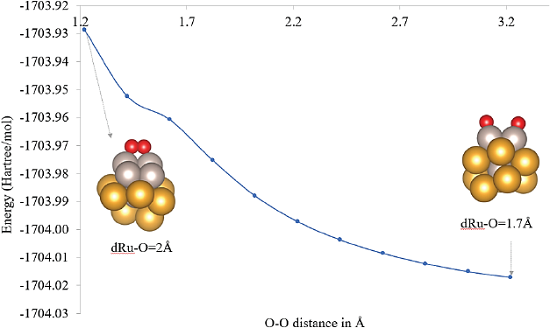
Color code: Au: yellow, Ru: gray and O: red.
Source: Author’s elaboration.
The adsorption profile shown in Figure 5, was computed by following the O2 distance coordinate. This leaded to a highly stable product of the dissociative O2 adsorption without an energy barrier.
The most stable structure in a quintet state is reported herein with a relative energy of -5.15 eV (-118.8 kcal/mol) at PBE-D3(BJ)/LANL2DZ level of theory for the highly exothermic dissociative chemisorption (structure 2c in Figure 5). The adsorption energies computed with a similar approach as that presented herein for different monometallic gold cluster models are presented in Table 3 for a comparative analysis.
Table 3 Adsorption energies for the oxygen molecule over gold clusters determined from first principles calculations as reported in previous studies. Relevant geometry parameters are presented.
Source: Author’s elaboration.
Structure
Geometry
Eads
r(O-O)
r(Au-O)
Ea(O-O)*
Method
Reference
Au13
hemispherical
-1.08
1.34
2.12
1.58
(Boronat y Corma, 2010)
Au25
cuboctahedral
-0.48
0.58
(Roldán et al., 2009)
Au38
cuboctahedral
-0.99
1.37
2.12
0.97
PAW-PW91
(Boronat y Corma, 2010)
Au38
cuboctahedral
-0.91
1.45
0.46
(Roldán et al., 2009>)
Au55
cuboctahedral
-0.24
0.74
(Roldán et al., 2009)
Au79
cuboctahedral
-0.19
1.46
0.41
(Roldán et al., 2009)
Au-nano
nanorrow
-0.92
1.31
1.44
(Roldán et al., 2009)
Au13
planar
-0.46
1.26
2.15
PW91/
(Yadav y Saini, 2020)
Au38
LANL2TZ
Au55
(f)-Au
Au79
6-311+G*-O
O2
octahedral
-0.82
(Liu et al., 2018)
octahedral
-0.20
PAW-PBE
(Liu et al., 2018)
octahedral
-0.30
(Liu et al., 2018)
-
1.21 exp
(Huber y Herzberg, 1979)
It is worth mentioning that the reported O2 adsorption energies to monometallic gold clusters are lower (less negative, see Table 1) than that computed for the Au-Ru cluster in the present contribution. As can be seen in Table 3, the O-O bond slightly elongated (<0.25 Å) when adsorbed to gold clusters, whereas the O-O distance in the adsorbed oxygen molecule to the bimetallic cluster is 3.7Å. Then the oxygen chemisorption is favored over the ruthenium sites, unlike gold clusters that need to overcome a high energy barrier for oxygen activation after adsorption, in the Au-Ru bimetallic cluster O2 is dissociated barrierless after adsorption.
An important property of the nanoparticle surface which influences its catalytic activity in heterogeneous phase is the bond strength and the chemical interactions with the reacting gas molecule. The surface interactions might stabilize a bond scission transition structure. The adsorbate-surface bond strength can be quantified through the calculation of the adsorption energy. Besides, to get insight into the adsorption of simple molecules on transition metal surfaces the d-band model is widely used. It enables to comprehend the trends in reactivity between the transition metals. The d-band model enhances the description of the adsorbate bond formation with a transition metal surface. It describes the interaction between the adsorbate valence states and d states of the transition metal surface. The differences in the interaction between the adsorbate and the transition metals arise due to formation of bonding and antibonding states between the valence states of the oxygen and the d states of the metal surface. The strength of the O-O bond is reduced by the filling of the antibonding states. In gas phase chemistry the occupation of states is determined by the number of electrons in the system, while in a metal surface the filling is given by the energy of the antibonding states relative to the Fermi level. The antibonding states are always above the d states. Then the energy of the d states (center of the d states) relative to the Fermi level is an indicator of the bond strength. As the d states are higher in energy with respect to the Fermi level (the energy difference between the d band center and the Fermi level decreases) the antibonding states are higher in energy (and emptier) then the surface-adsorbate bond is stronger.
To get a physical insight into the O2 interaction with Au, Ru or Au-Ru, the oxygen adsorption energies and d-band center (for the pristine structure) were computed for the monometallic Au13 or Ru13 clusters and the Au8Ru5 structure. The plot correlating these properties is presented in Figure 6.
Figure 6 Calculated adsorption energies of oxygen molecule as a function of the d-band center (eV) of the metal atoms in the cluster.

Source: Author’s elaboration.
The data displayed in Figure 6 can be explained through the d-band model. As can be seen an upshift in the d-band center (less negative value), found for the ruthenium cluster, corresponds to stronger oxygen adsorption strength (more negative adsorption energy). Whereas for the gold cluster the d-band center is lower in energy with respect to the Fermi level, then the oxygen adsorption is less strong than in Ru13. In the bimetallic structure the d-band center lies in an intermediate value between those obtained for the monometallic clusters, but closer to that found for Ru13.Then the adsorption energy behaves in a similar way and corresponds to a dissociative chemisorption (See 2c, Figures 7, 8).
Figure 7 a) Reaction profile and b) reaction scheme of first CO oxidation on Au8-Ru5 cluster.

Source: Author’s elaboration.
Figure 8 Reaction intermediates and transition structure detected for the CO oxidation.

Note: Some relevant geometry parameters (bond distances in Å and angle in degrees) are depicted.
Color code: oxygen: red, Au: yellow and Ru: gray.
Source: Author’s elaboration.
Once O2 is adsorbed, this 2c (Figure 7) highly stable intermediate enables the further reaction to evolve with exothermic character. The reaction profile and scheme of the initial CO oxidation cycle over the Au-Ru cluster are presented in Figure 7.
To explore the reaction route toward the CO oxidation a CO molecule was co-adsorbed on an interfacial gold atom, leading to the highly stable intermediate structure 3c.
As presented in Figure 8 the Ru-O bond distance of 1.71 Å is not affected by CO co-adsorption. The increase of the C-O bond distance is negligible (from 1.13 to 1.14 Å) after interacting with the Au atom in a similar fashion as that found in monometallic gold clusters.
By approaching the adsorbed CO* to the neighboring oxygen atom adsorbed on a Ru site a transition state (4cTS) was found and was confirmed through a frequency analysis ωimag = -281.15 cm-1 (See Figure 8). The energy barrier of 24.6 kcal/mol must be surmounted to reach the adsorbed product (see Figure 7a). This high barrier exceeds by far the ~5 to 6 kcal/mol needed for the CO oxidation on a highly active Au cluster (see activation energies shown in Table 4).
Table 4 Comparison of adsorption energies and activation energy for the CO oxidation over an Au cluster.
Source: Author’s elaboration.
Structure
Geometry
Eads O2
Eads CO
Ea(O-O)*
Method
Reference
Au38
octahedral
-0.82
-0.90
0.26
PAW-PBE
(Liu et al., 2018)
Au79
octahedral
-0.30
-0.77
0.23
(Liu et al., 2018)
For comparison, the reported activation energies for the O-O bond scission barrier from the OCOO* intermediate for octahedral NP model structures are presented in Table 4. (Liu et al., 2018). Conversely, a high CO oxidation barrier of 25.4 kcal/mol was reported for the neutral Ru cluster. (Zhang et al., 2014). Then in the bimetallic cluster, the presence of gold lowered this Ru energy barrier. An IRC calculation revealed an energy minimum connecting to the transition structure which corresponds to the CO2 adsorbed product (5c in Figure 6). This 5c product presents a bent CO2 molecule which deviates 44.5º from linearity and two nonequivalent C-O bond distances (1.20 Å, 1.27 Å) and is only 3.3 kcal/mol above the highly stable intermediate 3c.
Finally, the formed CO2 was desorbed to form product 6c. Therefore, the CO oxidation reaction over the free Au-Ru cluster might be thermodynamically controlled given that the CO oxidation barrier does not explain alone for the synergic effect that these systems might present. A second CO oxidation cycle was not explored in the present work. Other factors that may influence the reaction are the presence of additional reacting CO or O2 molecules and charge transfer effects from a support that may influence the undergoing reaction mechanism and that will be addressed in further contributions.
Conclusions
The present study provided a basic tool to build a nanoparticle model from scratch for computational modelling. Some properties that can be computed for the NPs model through a cluster approach and that are relevant for catalysis are presented. They are exemplified through the first principles-based study of a cuboctahedral Au-Ru cluster.
A metallic cluster was used as a model structure to get insight into the electronic properties, stability, and reactivity of Au-Ru bimetallic nanoparticles. A cuboctahedral Au8Ru5 structure was selected to explore the CO oxidation reaction based on its lowest formation enthalpy. Its higher stability agrees with reported experimental data of supported NPs. A high quintet state of the Au-Ru cluster was determined from first-principles calculations. Alike to ruthenium clusters, oxygen adsorbed dissociatively on a ruthenium site of the bimetallic cluster to a highly stable intermediate. The CO exothermic adsorption in the Au-Ru interphase produced a stable intermediate. The bimetallic cluster exhibited a greater preference toward O2 adsorption compared to an analogue monometallic Au cluster. The CO oxidation proceeded through a CO 2* adsorbed-like transition structure with an energy barrier of 24.6 kcal/mol to a product with a relative stability like that of the starting intermediate. The height of this barrier is lower than that determined in a Ru cluster, but higher than that reported for gold clusters.
The study of the isolated cluster provided a possible reaction pathway for the CO oxidation in the Au-Ru interface and enabled to determine the differences in properties compared to the monometallic clusters to get further comprehension of these kind of materials in catalysis.
References
- An, K., Somorjai, G. A. (2015). Nanocatalysis I: Synthesis of metal and bimetallic nanoparticles and porous oxides and their catalytic reaction studies. Catalysis Letters, 145(1): 233-248. https://doi.org/10.1007/s10562-014-1399-x
- Bhol, P., Bhavya, M. B., Swain, S., Saxena, M., Samal, A. K. (2020). Modern chemical routes for the controlled synthesis of anisotropic bimetallic nanostructures and their application in catalysis. Frontiers in Chemistry, 19(8): 357. https://doi.org/10.3389/fchem.2020.00357
- Blöchl, P. E. (1994). Projector augmented-wave method. Physical Review B, 50(24): 17953-17979. https://doi.org/10.1103/PhysRevB.50.17953
- Boronat, M., Corma, A. (2010). Oxygen activation on gold nanoparticles: separating the influence of particle size, particle shape and support interaction. Dalton Trans., 39(36): 8538-8546. https://doi.org/10.1039/C002280B
- Calzada, L. A., Collins, S. E., Han, C. W., Ortalan, V., Zanella, R. (2017). Synergetic effect of bimetallic Au-Ru/TiO2 catalysts for complete oxidation of methanol. Applied Catalysis B: Environmental, 207: 79-92.
- Calzada, L. A., Louis, C., Wan Han, C., Ortalan, V., Zanella, R. (2020). Au-Ru/TiO2 prepared by deposition-precipitation with urea: Relevant synthesis parameters to obtain bimetallic particles. Applied Catalysis B: Environmental, 264: 118503. https://doi.org/10.1016/j.apcatb.2019.118503
- Dimitratos, N., Lopez-Sanchez, J. A., Hutchings, G. J. (2012). Selective liquid phase oxidation with supported metal nanoparticles. Chemical Science, 3(1): 20-44. https://doi.org/10.1039/C1SC00524C
- Dovesi, R., Civalleri, B., Roetti, C., Saunders, V. R., Orlando, R. (2005). Ab initio quantum simulation in solid state chemistry. Reviews in Computational Chemistry, 1-125. John Wiley & Sons, Ltd. https://doi.org/10.1002/0471720895.ch1
- Ferrando, R., Jellinek, J., Johnston, R. L. (2008). Nanoalloys: from theory to applications of alloy clusters and nanoparticles. Chemical Reviews, 108(3): 845-910. https://doi.org/10.1021/cr040090g
- Freund, H.-J., Meijer, G., Scheffler, M., Schlögl, R., Wolf, M. (2011). CO oxidation as a prototypical reaction for heterogeneous processes. Angewandte Chemie International Edition, 50(43): 10064-10094. https://doi.org/10.1002/anie.201101378
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Scalmani, G., Barone, V., Petersson, G. A., Nakatsuji, H., Li, X., Caricato, M., Marenich, A. V, Bloino, J., Janesko, B. G., Gomperts, R., Mennucci, B., Hratchian, H. P., Ortiz, J. V, Fox, D. J. (2016). Gaussian16 Revision C.01.
- Garbounis, D. N., Tsipis, A. C., Tsipis, C. A. (2010). Structural, electronic, bonding, magnetic and optical properties of bimetallic ENT#091; Ru n Au m ENT#093; 0 / þ ( n þ m ≤ 3 ) clusters. Journal of Computational Chemistry, 31(16): 2836-2852. https://doi.org/10.1002/jcc.21575.31(16):2836-52
- Grimme, S., Antony, J., Ehrlich, S., Krieg, H. (2010). A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. Journal of Chemical Physics,132(15): 154104. https://doi.org/10.1063/1.3382344
- Grimme, S., Ehrlich, S., Goerigk, L. (2011). Effect of the damping function in dispersion corrected density functional theory. Journal of Computational Chemistry, 32(7): 1456-1465. https://doi.org/10.1002/jcc.21759
- Huber, K. P., Herzberg, G. (1979). Constants of diatomic molecules. In Molecular Spectra and Molecular Structure: IV. Constants of Diatomic Molecules, 8-689. Springer US. https://doi.org/10.1007/978-1-4757-0961-2_2
- Khandy, S. A., Islam, I., Gupta, D. C., Khenata, R., Laref, A. (2019). Lattice dynamics, mechanical stability and electronic structure of Fe-based Heusler semiconductors. Scientific Reports, 9(1): 1475. https://doi.org/10.1038/s41598-018-37740-y
- Kresse G., Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Physical Review B - Condensed Matter and Materials Physics, 59: 1758-1775.
- Kresse, G., Furthmüller, J. (1996a). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Computational Materials Science, 6(1): 15-50. https://doi.org/10.1016/0927-0256(96)00008-0
- Kresse, G., Furthmüller, J. (1996b). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Physical Review B, 54(16): 11169-11186. https://doi.org/10.1103/PhysRevB.54.11169
- Kresse, G., Hafner, J. (1993). Ab initio molecular dynamics for liquid metals. Physical Review B, 47(1): 558-561. https://doi.org/10.1103/PhysRevB.47.558
- Kresse, G., Hafner, J. (1994). Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Physical Review B, 49(20): 14251-14269. https://doi.org/10.1103/PhysRevB.49.14251
- Landman, U., Yoon, B., Zhang, C., Heiz, U., Arenz, M. (2007). Factors in gold nanocatalysis: oxidation of CO in the non-scalable size regime. Topics in Catalysis, 44(1): 145-158. https://doi.org/10.1007/s11244-007-0288-6
- Larsen, A. H., Mortensen, J. J., Blomqvist, J., Castelli, I. E., Christensen, R., Dułak, M., Friis, J., Groves, M. N., Hammer, B., Hargus, C., Hermes, E. D., Jennings, P. C., Jensen, P. B., Kermode, J., Kitchin, J. R., Kolsbjerg, E. L., Kubal, J., Kaasbjerg, K., Lysgaard, S., Jacobsen, K. W. (2017). The atomic simulation environment a Python library for working with atoms. Journal of Physics: Condensed Matter, 29(27): 273002. https://doi.org/10.1088/1361-648x/aa680e
- Liu, J.-X., Filot, I. A. W., Su, Y., Zijlstra, B., Hensen, E. J. M. (2018). Optimum particle size for gold-catalyzed CO oxidation. The Journal of Physical Chemistry C, 122(15): 8327-8340. https://doi.org/10.1021/acs.jpcc.7b12711
- Louis, C. (2007). Gold nanoparticles: recent advances in CO oxidation. Nanoparticles and Catalysis, 475-503. https://doi.org/https://doi.org/10.1002/9783527621323.ch15
- Lu, B.-J., Li, X.-T., Zhao, Y.-J., Wang, Z.-Y.,Yang, X.-B. (2017). Structural stabilities and electronic properties of Mg28-nAln clusters: A first-principles study. AIP Advances, 7(9): 95023. https://doi.org/10.1063/1.5000792
- Miedema, A. R., de Boer, F. R., de Chatel, P. F. (1973). Empirical description of the role of electronegativity in alloy formation. Journal of Physics F: Metal Physics, 3(8): 1558-1576. https://doi.org/10.1088/0305-4608/3/8/012
- Momma, K., Izumi, F. (2011). Vesta for three-dimensional visualization of crystal, volumetric and morphology data. Journal of Applied Crystallography, 44(6): 1272-1276. https://doi.org/10.1107/S0021889811038970
- Nasrabadi, H. T., Abbasi, E., Davaran, S., Kouhi, M., Akbarzadeh, A. (2016). Bimetallic nanoparticles: Preparation, properties, and biomedical applications. Artificial Cells, Nanomedicine and Biotechnology, 44(1): 376-380. https://doi.org/10.3109/21691401.2014.953632
- Perdew, J. P., Ruzsinszky, A., Csonka, G. I., Vydrov, O. A., Scuseria, G. E., Constantin, L. A., Zhou, X., Burke, K. (2008). Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett., 100(13): 136406. https://doi.org/10.1103/PhysRevLett.100.136406
- Prati, L., Villa, A., Jouve, A., Beck, A., Evangelisti, C., Savara, A. (2018). Gold as a modifier of metal nanoparticles: effect on structure and catalysis. Faraday Discussions, 208: 395-407. https://doi.org/10.1039/C7FD00223H
- Pundlik, S. S., Kalyanaraman, K., Waghmare, U. V. (2011). First-principles investigation of the atomic and electronic structure and magnetic moments in gold nanoclusters. The Journal of Physical Chemistry C, 115(10): 3809-3820. https://doi.org/10.1021/jp102482g
- Roldán, A., González, S., Ricart, J. M., Illas, F. (2009). Critical size for O2 dissociation by Au nanoparticles. ChemPhysChem, 10(2): 348-351. https://doi.org/https://doi.org/10.1002/cphc.200800702
- Stradi, D., Jelver, L., Smidstrup, S., Stokbro, K. (2017). Method for determining optimal supercell representation of interfaces. Journal of Physics: Condensed Matter, 29(18): 185901. ArXiv.
- Tojo, C., Buceta, D., López-Quintela, M. A. (2017). On metal segregation of bimetallic nanocatalysts prepared by a one-pot method in microemulsions. Catalysts, 7(2): 68. https://doi.org/10.3390/catal7020068
- Yadav, J., Saini, S. (2020). Atop adsorption of oxygen on small sized gold clusters: Analysis of size and site reactivity from restructuring perspective. Computational and Theoretical Chemistry, 1191: 113014. https://doi.org/https://doi.org/10.1016/j.comptc.2020.113014
- Yao, Y., Huang, Z., Hughes, L. A., Gao, J., Li, T., Morris, D., Zeltmann, S. E., Savitzky, B. H., Ophus, C., Finfrock, Y. Z., Dong, Q., Jiao, M., Mao, Y., Chi, M., Zhang, P., Li, J., Minor, A. M., Shahbazian-Yassar, R., Hu, L. (2021). Extreme mixing in nanoscale transition metal alloys. Matter, 4(7): 2340-2353. https://doi.org/10.1016/j.matt.2021.04.014
- Zaleska-Medynska, A., Marchelek, M., Diak, M., Grabowska, E. (2016). Noble metal-based bimetallic nanoparticles: the effect of the structure on the optical, catalytic and photocatalytic properties. Advances in Colloid and Interface Science, 229, 80-107. https://doi.org/https://doi.org/10.1016/j.cis.2015.12.008
- Zhang, S.-T., Li, C.-M., Yan, H., Wei, M., Evans, D. G., Duan, X. (2014). Density functional theory study on the metal-support interaction between Ru cluster and anatase TiO2(101) surface. The Journal of Physical Chemistry C, 118(7): 3514-3522. https://doi.org/10.1021/jp409627p
Annex
Coordinates generated in a xyz file
Cuboctahedron Au 13
13
Lattice = “4.08 0.0 0.0 0.0 4.08 0.0 0.0 0.0 4.08” Properties = species:
S:1:pos:R:3 pbc = “F F F”
Cuboctaedron Au 55
55
Lattice = “8.16 0.0 0.0 0.0 8.16 0.0 0.0 0.0 8.16” Properties = species:
S:1:pos:R:3 pbc = “F F F”