www.mundonano.unam.mx | Mundo Nano
http://dx.doi.org/10.22201/ceiich.24485691e.2022.29.69699 | 15(29), 1e-19e, julio–diciembre 2022
Review articles
Oligomeric approach to 2D materials modeling◊
Enfoque oligómero para simulación de materiales 2D
Serguei Fomine*♦
Wilmer Esteban Vallejo Narváez*
César Gabriel Vera de la Garza*
Luis Daniel Solís Rodríguez*
* Universidad Nacional Autónoma de México, Instituto de Investigaciones en Materiales.
♦ Correspondence author: fomine@unam.mx
Abstract:
Oligomeric approach has been originally developed to study electronic properties of conjugated polymers. This approach allows to access electronic properties of 1D systems otherwise difficult to calculate. We successfully extended this method to study electronic properties of 2D materials. In this review we summarize our recent work in this area. It has been established that large graphene nanoflake possess multiconfigurational singlet or even high spin ground state. Doping of 2D systems has also been explored and it has been demonstrated that doping allows to tune their electronic properties, including ionization potentials, electron affinities, reorganization energies and the very nature of the ground state. The electronic properties of novel 2D allotropies of carbon, phosphorus, germanium and silicon have been studied as well as their complexes with Li. Heterostructures, of different 2D allotropies are readily formed. This is an alternative method for tuning of their electronic properties.
Keywords: 2D-materials, nanoflakes, graphene allotropies, oligomeric approach, density functional theory.
Resumen:
El enfoque oligomérico se desarrolló originalmente para estudiar las propiedades electrónicas de los polímeros conjugados. Este método permite acceder a las propiedades electrónicas de los sistemas 1D que de otro modo son difíciles de calcular. Hemos empleado con éxito este método para estudiar las propiedades electrónicas de materiales 2D. En la presente revisión presentamos nuestro trabajo reciente en esta área. Se ha establecido que las nanohojuelas de grafeno grandes poseen estado fundamental multiconfiguracional o incluso uno de alto espín. También, se ha estudiado el dopaje de sistemas 2D y se ha demostrado que este permite modificar sus propiedades electrónicas, tales como los potenciales de ionización, afinidades electrónicas, energías de reorganización y la naturaleza del estado fundamental. Se han estudiado las propiedades electrónicas de las nuevas formas alotrópicas 2D de carbono, fósforo, germanio y silicio, así como sus complejos con Li. Se encontró que se forman fácilmente heteroestructuras de diferentes alotropías 2D. Este es un método alternativo para la modulación de propiedades electrónicas de dichas formas alotrópicas.
Palabras clave: materiales 2D, nanohojuelas, grafeno, formas alotrópicas, enfoque oligómero, teoría de funcionales de la densidad.
Received: September 2, 2021.
Accepted: November 15, 2021.
Introduction
It can be said that nowadays the world of materials undergoes a silent revolution. The revolution is dual, consisting of size and dimension change. Electronic devices grow smaller and 2D materials gain their importance. A few decades ago, the mainstream of materials science were 3D and 1D materials: solids and polymers, respectively. Their properties were very well studied and understood, and their weak and strong sides were completely recognized. It was not until 1986 (Joensen et al., 1986) when the first 2D material (MoS2) was synthesized, that scientific community starts viewing 2D materials as something worth studying. However, the real shift of scientific paradigm arrived in 2004, after graphene discovery (Novoselov et al., 2004). It has been perceived that 2D materials combine the best of two worlds - the worlds of 1D and 3D materials. At the same time the bottom-up approach was taking over the top-down one in materials science stimulated by fundamental limitations of further device miniaturization in microelectronics. These two global tendencies have brought interest of many researchers to nanoscopic 2D systems. It is well recognized that nanoparticles possess qualitatively different properties from those of bulk, due to much higher ratio of the number of surface atoms to the number of bulk atoms. This makes modeling of nano systems quite a challenging task. If we consider conventional modeling methods for solids; periodic boundary condition (PBC) methods which are widely applied to solids, polymers and infinite 2D systems, they are incapable to capture the nano size effects. PBC methods use translational symmetry to define 3D, 2D or 1D systems and cannot describe the effect of quantum confinement and surface atoms. The supercell approach is not very helpful either since it drastically increases the computational demands and impractical for nano sized systems. Moreover, PBC approach is intrinsically uncapable to provide such an important information as ionization potentials, electron affinities and relaxation energies. An obvious alternative to PBC method -direct optimization of a nanocluster is still out of reach for modern computers, since a nanoparticle may contain much more than several thousand of atoms a practical limit for nowadays computers. However, there is a workaround for this problem; so-called oligomeric approach which has been successfully used for a long time to study electronic properties of conjugated polymers (Zade et al., 2011). It consists in the calculation of electronic properties of increasing size oligomers and then extrapolating these properties to the infinite system. Similar approach can be used for nanosized 2D systems too. Moreover, nanosized 2D systems of graphene, doped graphene and other 2D nanoflakes are interesting objects on its own due to notable influence of size on their electronic properties. In this work we would like to review our research of the last years to show how the oligomeric approach can be applied to 2D nano systems to explore their electronic properties.
Graphene nanoflakes
A systematic study of the electronic structure of polycyclic hydrocarbons from naphthalene to a system containing up to 80 fused benzene rings has been conducted (Torres, Guadarrama and Fomine 2014) (Figure 1). Geometries were optimized for closed shell singlet, open shell singlet, triplet and multiplet states at B3LYP/cc-pVDZ level of theory. Complete active space self-consistent field (CASSCF) (10,10)/6-31G(d) single point energy evaluation has been carried out for all optimized structures. The complete active space and D1 diagnostic calculations (Hättig, 2003) demonstrated that for graphene nanoflakes containing more than 40 fused benzene rings the ground state becomes multiconfigurational. The largest nanoflakes (NFs) can be defined as polyradicals. Because of this fact single determinant methods should be used with caution for large polycyclic hydrocarbons including graphene (NFs). However, we would like to note that multiconfigurational character does not necessarily means the polyradical state.
Figure 1 Studied graphene NFs of different sizes starting from naphthalene.

Note: Two types of NFs have been explored: NFs with long zigzag and long armchair edges, respectively.
Source: Author’s elaboration.
All medium size graphene NFs have multiconfigurational singlet ground state. It has only two dominant configurations: ground state singlet and doubly excited singlet. Thus, small polycyclic hydrocarbons have mostly closed shell singlet ground state, the medium size systems have notable multiconfigurational ground state (singlet or triplet) with only moderate polyradical character. The ground state of the largest systems is open-shell singlets with poly-radical characters.
Nitrogen doping can be used to tune the electronic structure of graphene NFs (Torres and Fomine, 2015). Hybrid B3LYP (Becke, 1993) double hybrid B2LYP (Zhang et al., 2009) functionals and CASSCF (Hegarty & Robb, 1979) methods have been used for this study (Figure 2).
Figure 2 Nitrogen doped graphene NFs. 1-pyridinic nitrogen. 2-graphitic nitrogen.

Source: Author’s elaboration.
In all but one case, the restricted B3LYP solutions showed triplet instability and the CASSCF calculations provided evidence for multiconfigurational nature of the ground state, with contributions from two dominant configurations. It is interesting to note that doping does affect the multiconfigurational character of the NFs in their neutral state. The relative stability of doped NFs depends mostly on the mutual position of the dopant atoms and much less on the position of nitrogen atoms within the NF. N-graphitic doping affects the cationic states notably more than anionic ones, due the participation of the nitrogen atoms in the stabilization of the positive charge, resulting in a drop of ionization potentials (IPs) for N-graphitic doped systems. Nitrogen atoms do not participate in the negative charge stabilization of anionic species and, therefore, the doping does not affect the electron affinities (EAs). The unrestricted B3LYP method is the method of choice for the calculation of IPs, EAs and reorganization energies. Restricted B3LYP and B2PLYP produce less reliable results for both IPs and EAs, while CASSCF strongly underestimates the electron affinities. This shortcoming of CASSCF could be overcome using a perturbative correction to the CASSCF energy. However, the computational cost of this correction is prohibitively high to implement for such large systems. B2PLYP poor results are probably due to the low ‘‘quality’’ of the closed shell reference wavefunction and lack of static correlation. This is also true for reorganization energies where restricted B3LYP produces qualitatively incorrect results. Doping changes the reorganization energy of the nanoflakes; the hole reorganization energy is generally higher than the corresponding electron reorganization energy due to the participation of nitrogen atoms in the stabilization of the positive charge. Single determinant methods do not provide meaningful description for neutral species, however, for the ionic species this is not the case and single determinant methods give a reasonable description. As a result, single determinant methods do not provide a well-balanced description for both structures, giving too low IPs and too high EAs. They notably overestimate the energy of neutral species. Depending on the type of doping, nitrogen atom (pyridinic or graphitic) can be p or n type dopant, respectively.
Boron is another element which can be used to tune the properties of graphene NFs (Torres, Flores, Fomina et al., 2016). Boron is located just before carbon in the Periodic Table, while nitrogen is followed by carbon. Nitrogen has an extra electron compared to carbon, while boron has one electron less than carbon. B3LYP and CASSCF methods were applied to study graphene NFs doped with boron atoms. Both methods DFT and CASSCF agree on the relative stability of studied isomers. Figure 3 shows the studied NFs.
Figure 3 Positions of boron atoms in graphene NFs.

Note: There are 2 boron atoms per NF, their positions are marked by the same letters.
Source: Author’s elaboration.
The restricted B3LYP solutions were found to be unstable in all but two cases, and CASSCF calculations prove the multiconfigurational character of the ground states contributing with two most important configurations. The distance between dopant atoms, their mutual positions and their locations within the nanoflake impacted the relative stability of doped systems. Thus, for the models where boron atoms are well separated from one another, the ground state is single configurational. Boron doping does not modify the IPs of doped nanoflakes. However, it notably increases the EAs of core-doped nanoflakes presumably due to reduction of total electron repulsion energy in doped systems. The doping has a notable impact on the reorganization energy of the NFs too. Doping changes the reorganization energies of boron doped NFs which are always higher than the reorganization energies of pristine- and N-doped NFs. Moreover, the core-doped NFs have higher reorganization energies compared to the edge-doped ones. The presence of the empty p-orbitals on B atoms in the core-doped nanoflakes also notably increases EAs of boron doped systems compared to nitrogen doped ones, confirming p -type doping for core-doped systems. It is interesting to note that all triplets are single configurational states since static correlation is less important for triplets compared to singlets (Torres et al., 2014).
The understanding of the fundamental differences between 1D and 2D systems is very important for the device design, therefore, it has been conducted a comparative study of 1D and 2D π-conjugated systems at D3bj dispersion corrected (Grimme et al., 2010) B3LYP and restricted active space (RAS) levels of theory, using oligomeric approach. Two sets of systems differing by the connection density have been studied (Figure 4). The connection density of atom A represents the number of atoms of the same type forming covalent bonds with atom A. Thus, the connection density for carbon atom in graphene is 3, in polyacetylene is 2. Explored systems were poly-m -phenylene (1D-PMP) and the corresponding 2D analogue: porous graphene (2D-PMP). The second one is trans-polyacetylene (1D-PA) oligomers and graphene nanoflakes(2D-PA).
Figure 4 Studied 1D and 2D conjugated systems.

Source: Author’s elaboration.
The difference between 1D and 2D conjugated systems depends on the connection densities in 2D systems. Higher connection density implies greater differences between 1D and 2D electronic structures. The difference between 1D and 2D-PMP lies in smaller bandgaps (Egs), and higher IP’s and EA’s for 2D-PMP of similar sizes. 2D-PMP systems have higher IPs, EAs and lower Eg than 1D-PMP of the similar size. The ground state is closed shell singlet for both 1D and 2D-PMP. The difference between 1D and 2D-PA is much more striking and mostly related with the nature of the ground states of 2D-PA, varying from closed shell singlet to multiconfigurational singlet states and further to the high spin ground states. They possess from 4 to 12 unpaired electrons depending on the size of 2D-PA. Both RAS and DFT calculations confirm the high spin nature of the ground states for large 2D-PAs. On the other hand, 1D-PAs have a closed singlet ground state independently on the size of the oligomer. The higher connection density in 2D-PA affects not only the nature of the ground states but also the Egs and EAs. Eg drops much more rapidly for 2D-PA with size than for 2D-PMP and EAs of 2D-PA are always lower than these of 1D-PA of the same size due to greater electron repulsion.
Another important difference between 1D and 2D conjugated oligomers is the existence of high spin ground states for the latter. It has been studied the effect of the substituents on the electronic properties of graphene nanoflakes possessing high spin ground state, using D3bj dispersion corrected (Grimme et al., 2010) B3LYP functional in combination with cc-pVDZ basis set as well as CASSCF methods (Torres, Flores and Fomine, 2016).
Figure 5 Graphene nanoflake showing high spin ground state.

Source: Author’s elaboration.
The results of DFT and CASSCF calculations qualitatively agree with each other. It has been found that the origin of high spin ground states is due to non-disjoint character of highest SOMO’s orbitals, causing strong exchange coupling between electrons. This explains the violation of the Ovchinnikov rule (Ovchinnikov, 1978). It is interesting to note that the substituents affect the nature of the ground state. The electron withdrawing substituents, especially these with cyano groups favor the singlet ground state. The effect of the electron donating groups is more erratic. They can promote both high and low spin ground states. The side groups affect the topology of single occupied molecular orbitals, modifying the exchange interactions. Hence, depending on the type of substituents, one or another spin state could be favored. The substitution of the nanoflake increases the reorganization energies which could be connected to the less rigid structure of the NFs bearing side groups compared to pristine NF. The rise of the reorganization energy also depends on the substituent nature. However, both, withdrawing and electron donating substituents increase the reorganization energies as well as Egs.
Silicene nanoflakes
Other elements such as silicon and phosphorus are also known to form 2D structures, therefore, the electronic properties of rectangular silicene nano clusters (nanoflakes) with hydrogen passivated edges with two zigzag and two armchair edges have been explored (Pablo-Pedro et al., 2017).
Figure 6 An example of studied silicene nanoflake.

Source: Author’s elaboration.
By using DFT and CASSCF methods we have found that for the nanoflakes where zigzag edge is larger than the armchair one, the ground state is a singlet (S = 0). However, a switching from a singlet (S = 0) to a triplet (S = 1) ground state is observed when zigzag side becomes larger than the arm-chair edge. Modeling of Raman spectrum revealed that, the S = 0 and S = 1 ground states can be characterized by E2g (G) and A (D) Raman modes. Furthermore, silicene nanoflakes are shown to have HOMO-LUMO energy gaps, which decrease as a function of number of atoms of edges for both singlet and triplet ground states. Silicene nanoflakes with a S = 1 ground state can be potentially used for silicene-based spintronic devices.
Since high-performance materials rely on small reorganization energies to facilitate both charge separation and charge transport, DFT calculations have been performed to estimate reorganization energies silicene nanoflakes. It was observed that across all geometries, silicene nanoflakes feature larger electron affinities and highly stabilized anionic states, indicating their potential as n -type materials. These findings suggest that fine-tuning of the size of nanoflakes along the “zigzag” and “armchair” directions may permit the design of novel n -type electronic materials and spintronics devices that incorporate both high electron affinities and very low internal reorganization energies (Pablo-Pedro et al., 2018).
Phosphorene nanoflakes
Phosphorus is another element readily forming 2D structures (phosphorene). Hydrogen passivated phosphorene NFs of different shapes and sizes have been explored using dispersion corrected (Grimme et al., 2010) BHan-dHLYP hybrid functional (Olmeda et al., 2018).
Figure 7 Smallest and largest phosphorene nanoflakes of each type used for the study.

Source: Author’s elaboration.
It is known that this functional accurately reproduces the experimental bond lengths and valence angles of black phosphorus. As expected, all NFs were found to have singlet ground state and their Egs decrease linearly with 1/N, where N is the number of P atoms in the NF. This behavior resembles that of organic conjugated polymers due to the overlapping of 3pz orbitals of the P atoms. It seems that the topology of the nanoflake edges does not affect Eg. IPs and EAs generally grow smaller with increasing of nanoflake size. The change in IPs and EAs with size correlates with the delocalization pattern of polaron cations and anions in the nanoflakes. Shape and nature or the longest edge (zigzag or armchair) affect both the IP and EA. Square nanoflake always have lower Eg than rectangular nanoflakes with the same number of atoms due to larger number of connections per atom. Theoretically calculated low hole reorganization energies (less than 0.1 eV) agree well with experimentally determined high hole mobility in phosphorene (Liu et al., 2014). The low hole reorganization energies are due to the better ability of phosphorene nanoflakes to delocalize polaron cations compared to polaron anions.
Properties of phosphorene can also be modified by doping. These properties tuning by Al and Si doping has been studied using hybrid functional BHandHLYP and CASSCF methods (Olmedo et al., 2019). The examples are shown in Figure 8.
Figure 8 Geometry of the most heavily doped phosphorene nanoflakes with aluminum (1) (aluminum atoms shown in black) and silicon (2) (silicon atoms shown in gray).

Source: Author’s elaboration.
Doping of phosphorene NFs with Al and Si changes NF geometry, it increases the bond length alternation and change NF shape. Doped NFs adopt waveshape-like geometry, which is most notable for Al doping, these effects grow with the doping level. All dopant atoms are positively charged in doped NFs, Al being about twice as positive as Si due to lower electronegativity. Doping also decreases singlet-triplet splitting in the NFs. This effect is most notable for Si doping where singlet and triplet states become virtually degenerated. Doping also reduces band gaps and changes the nature of the ground states for Si-doped systems. The ground state of Si-doped NFs becomes polyradical, in which unpaired electrons are located at Si atoms. Generally, odd number of valence electrons at a dopant atom leads to closed-shell ground state, while even number produces polyradical ground state in case of phosphorene. Doped systems show increased EAs, while the IPs are much less affected. The reason for this is that cation polarons are mostly localized over P atoms, whereas polaron anion delocalization involves 3pz orbitals of dopant atoms. Doping also impacts the reorganization energies increasing them for all dopant types. Al-doped systems can still be considered as hole transport materials like phosphorene, while Si doping produces materials with similar reorganization energies for both electrons and holes and in some cases can they be considered as electron transport materials. The edge doping results in less stable systems than core doping for both Al and Si. Moreover, edge-doped systems show higher reorganization energies and are less relevant than core doped nanoflakes due to higher total energies.
To understand the evolution of the properties of the NF within third dimension, phosphorene monoflakes (Mfs) and biflakes (Bfs) doped with Al, Si, and S atoms have been explored focusing on their structural features and electronic properties (De la Garza, Rodriguez et al. 2021). These systems were examined using TPSS meta GGA functional coupled with def2-SVP basis set, CASSCF method has also been used. The results indicate that Al and Si substitution produces significant structural distortions in both Mfs and Bfs compared to S- substituted and pristine systems. Specifically, Al, Si and S cause a drop in Eg and IPs and an increase of EAs compared to pristine Mfs. In addition, Al doping enhances the hole mobility in the Mfs, while S and Si doping affects similarly EAs and reorganization energies.
In case of Bfs, Si-Si and Al-P interlaminar interactions were observed, which cause structural distortions due to high binding energies for Si and Al doped Bfs. Si doping does not generate substantial alterations in Egs. However, it leads to high hole mobility, which is not the case for Si-Mfs. Furthermore, Si and Al doping increases IP of Mfs compared to Bfs, which is observed over the entire range of studied doping concentrations. For EAs, all Bfs follow the tendency noted for their monolayer counterparts. Al doped Bfs exhibit high hole mobility, while there was no correlation between doping level and reorganization energies for the system containing sulfur. These results suggest that the Eg of phosphorene can be tuned depending on the dopant type and doping level.
Figure 9 Monoflakes (Mfs) and biflakes (Bf) under study.

Source: Author’s elaboration.
2D carbon allotropies
2D systems could possess different topologies, not necessarily only honeycomb structure comprising fused hexagons like graphene, silicene or phosphorene, although these are the most stable 2D allotropies. 2D structure could be formed by a mix of different type of polygons and the second most stable 2D allotropy of carbon called haeckelites is formed by fused azulene structures, representing a combination of fused pentagon and heptagon rings (Enyashin and Ivanovskii, 2011). These structures are occurred naturally as defects in graphene and known as Stone-Wales defects (Chuvilin et al., 2009). A comparative theoretical study of graphene NFs and isomeric NFs (H1 and H2) based on dispersion corrected hybrid DFT and CASSCF calculations has been conducted to access the electronic properties of isomeric NFs (De la Garza et al., 2018). Their structures are shown in Figure 10.
Figure 10 Largest studied haeckelite NFs of different types: H1 and H2 together with largest studied isomeric graphene nanoflake.

Source: Author’s elaboration.
As expected, two types of haeckelites nanoflakes H1 and H2 were found to be less stable compared to isomeric graphene NFs at all theoretical levels. H1 and H2 have closed shell singlet ground state independently on their size and strong bond length alternation. For all types of NFs, the evolution of their IPs, EAs and Eg with size is similar. IP and Eg drop, and EA increases with NF size. H1 and H2 show lower IPs and Eg and higher EAs compared to the corresponding graphene NF of the same size. However, IPs, Eg and EAs converge with size for all three types of the NFs becoming virtually identical for the largest representatives of H1, H2 and graphene NF. H1 and H2 NF types have a non-uniform distribution of the electron density across the NF, unlike graphene systems, which makes them promising candidates for regioselective chemical modification. All types of NFs; graphene and haeckelite were shown to have singlet ground states, although singlet-triplet gap drops notably with the NF size. Small NFs of all types have closed shell singlet ground state. The difference between the ground state natures of both NF types becomes evident for large NFs; large graphene NFs have polyradical antiferromagnetic ground state, while even large haeckelite NFs maintain closed shell singlet ground state. This difference is originated from the bond length alternation (BLA) pattern. Haeckelite NFs have large BLA independently on their size, while graphene NFs show small BLA pattern. Graphene NFs are more stable than the corresponding haeckelites, H2 being more stable than H1, in accordance with known DFTB data (Enyashin and Ivanovskii, 2011) for the infinite 2D systems.
Both, graphene and haeckelites are carbon allotropies, therefore, the electronic properties of the latter can also be tuned by doping with boron and (or) nitrogen. This hypothesis has been explored using dispersion corrected B3LYP functional and CASSCF methods where H1 and H2 nanoflakes were doped by 2 atoms of boron or 2 atoms of nitrogen (De la Garza et al., 2019). Figure 11 shows the most stable doped structures for each type of doping.
Figure 11 The most stable nitrogen and boron doped haeckelite NFs.
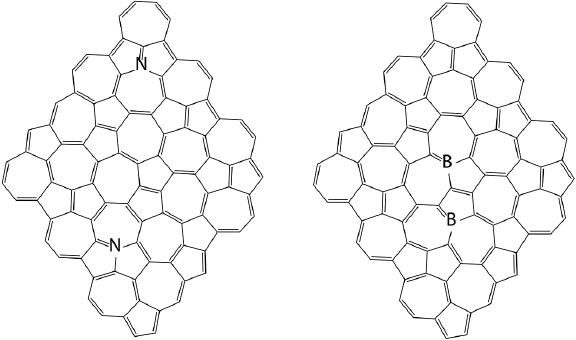
Source: Author’s elaboration.
The most stable N and B-doped NFs have common substitution patterns: the most thermodynamically stable isomers of nitrogen and boron doped systems contain phenalene and azulene motifs substituted in positions 7 and 9, respectively. All the most stable isomers are H2 systems. The difference in the relative energies between isomers can be as high as 40 kcal/mol. It was found that nitrogen doping promotes NF planarity, increases singlet-triplet gap and band gap, while boron doping promotes dome shaped NF geometry. This effect depends on the distance between the dopant atoms. Closely located dopant atoms have stronger effect on the NF shape compared to separated dopant atoms. In general, isomeric nanoflakes are less sensitive to doping compared to graphene NFs. Boron and nitrogen doping produce different effects on the electronic structure of H1 and H2 NFs. Nitrogen atoms promote closed singlet ground state, they increase singlet - triplet gap, and Eg, boron decreases singlet - triplet energy gap and in some cases promotes polyradical ground states. IP and EA of H1 and H2 NFs are less affected by doping compared to graphene NF too. Nitrogen can still be considered as n dopant for H1 and H2 NFs, while boron cannot be considered as p type of dopant for isomeric graphene NFs. The probable reason for this behavior is so called “internal” doping of isomeric graphene NFs when the same type of atoms become chemically different. Non uniform electron density distribution in these NF decreases the effect of heteroatom doping on the electronic properties.
Simultaneous and heavy doping of carbon allotropies with boron and nitrogen leads to the formation of hybrid materials. B3LYP-D/def2-SVP level of theory was utilized to study their properties (De la Garza et al., 2020). The doping of NFs (H1 and H2 in Figure 12) notably alters the geometry. The difference is due to distinct symmetries of allotropic NFs. Simultaneous boron and nitrogen doping promotes polyradical antiferromagnetic ground states in the NFs and affects the nanoflake electronic structure. Pristine H1 and H2 NFs have singlet closed-shell ground states, while doped NFs exhibit from 1 to 6 unpaired electrons in their ground states. The number of unpaired electrons rise with the deviation from plane for all doped NFs. A notable charge transfer occurs from boron to nitrogen atoms, which increases with doping level. Boron atoms become positively charged while nitrogen atoms developed negative charges. Boron and nitrogen doping alters IPs and EAs. Boron barely modifies either IPs or EAs being neither n nor p dopant. The band gap of doped NFs generally increases with the number of dopant atoms. The reorganization energies also grow with combined doping level, which is related to higher polaron localization in doped systems. The hole reorganization energies were generally lower than the electron reorganization energies; consequently, these materials can be considered hole-transporting structures.
Figure 12 Allotropes H1 and H2 doped with boron and nitrogen atoms.

Source: Author’s elaboration.
Heterostructures
Another method of 2D allotropies property tuning is the formation of heterostructures (HSs) by 2 different types of 2D materials bounded together by some type of interaction. This method of modification of the electronic properties has been studied using phosphorene, graphene, H1 and H2 nanoflakes (Narváez et al., 2020) (Figure 13). Their corresponding complexes with Li have been analyzed too using dispersion-corrected TPSS functional with def2-SVP basis set. According to the results, HSs are bounded together mainly by dispersion. The interaction is very substantial, reaching more than 140 kcal/mol for a NF pair. The charge transfer in neutral HSs is minimal due to the nature of the interactions. On the other hand, the interaction energy between the NFs and Li atoms increases in the following order phosphorene = H2 = H1 > graphene. There is a synergetic effect for Li binding energies in HSs. This outcome is most significant for the phosphorene binding sites; but it also stands for graphene, H1, and H2 NFs. The binding with Li always conduces to the almost complete charge transfer from Li to the NFs or HSs. For HSs, the unpaired electron of Li is always located at the carbon NF side independently of the Li binding location. The formation of Li complexes follows the same pattern for both NFs and HSs. The mutual influence of NFs in the HSs results in a synergetic effect increasing Li interaction energies and the activation energies of hopping compared with individual NFs. This impact is most relevant for phosphorene binding sites. The energies of Li hopping for individual NFs are notably higher for phosphorene nanoflakes compared to graphene, H1, or H2 NFs. The formation of HSs increases moderately activation energies of Li hopping due to higher Li binding energies in HSs compared to individual NFs.
Figure 13 (Top) Studied species: phosphorene (P), graphene (G), allotropes H1 and H2; (bottom) heterostructures (HSs) and studied lithium complexes.

Source: Author’s elaboration.
Si, P and Ge analogs of haeckelites
Large structural flexibility presented by 2D materials is an indispensable characteristic in materials design. Despite its importance, finding arrangements with proper stability remains a notable challenge. It has been found that silicon, phosphorus and germanium can form inorganic haeckelite analogues (Figure 14). Both 2D structures and NFs are structurally stable (De la Garza, Narváez et al., 2021). They can form H1 and H2 types of allotropes. The relative stability of inorganic H1 and H2 allotropies is particularly higher compared to carbon haeckelites. All 2D materials except phosphorus analogs exhibited metallic behavior; nevertheless, the difference between inorganic haeckelites and the corresponding honeycomb structures is less than that between haeckelites and graphene. According to the results, there is a significant difference between carbon and inorganic allotropies; the latter exhibiting higher electron affinities achieving nearly 4 eV for Ge allotropies because of the participation of 3d orbitals in the negative charge stabilization. In all cases, H1 and H2 always show higher EAs, and lower IPs compared to honeycomb structures. Inorganic H1 and H2 allotropies show increased affinity to lithium atoms compared to honeycomb geometries in all studied cases. Overall, these novel structures are promising materials for applications in Li-ion batteries due to the high Li atoms affinities and low hopping activation energy.
Figure 14 Geometries of haeckelites and their inorganic analogues.

Source: Author’s elaboration.
Conclusions
The oligomeric approach is a powerful tool allowing to study a variety of important properties of 2D materials and nanoflakes using advanced procedures not available within PBC framework, allowing deeper insight into electronic structure of 2D objects. It has been found out that large graphene nanoflake have multiconfigurational singlet or sometimes high spin ground state and could be promising materials for their applications in spintronic devices. Doping of 2D materials allows to tune their electronic properties, changing IPs, EAs, reorganization energies and the nature of the ground state. Oligomeric approach allows for discovery and exploring properties of unconventional 2D allotropies not only for carbon (haeckelites) but also for other elements such as silicon phosphorus and germanium. Haeckelites are the second most stables 2D allotropies for all these elements after honeycomb structures, they are structurally stable, possess higher electron affinities lower ionization potentials and high affinity to lithium atoms which is important por potential applications. The electronic properties haeckelites can be modified by doping, in line with honeycomb allotropies. Moreover, different 2D allotropies can form heterostructures, allowing to tune their electronic properties and their geometries.
References
- Becke, A. D. (1993). Density‐functional thermochemistry. III. The role of exact exchange. The Journal of Chemical Physics, 98(7). https://doi.org/10.1063/1.464913
- Chuvilin, A., Meyer, J. C., Algara-Siller, G., Kaiser, U. (2009). From graphene constrictions to single carbon chains. New Journal of Physics, 11(8): 083019. https://doi.org/10.1088/1367-2630/11/8/083019
- De la Garza, C. G. V., García, G. L., Olmedo, E. M., Peña, E. R., Fomine, S. (2018). Electronic structure of isomeric graphene nanoflakes. Computational and Theoretical Chemistry, 1140: 125-133. https://doi.org/10.1016/j.comptc.2018.08.007
- De la Garza, C. G.V., Olmedo, E. M., Fomine, S. (2019). Electronic structure of boron and nitrogen doped isomeric graphene nanoflakes. Computational and Theoretical Chemistry, 1151: 12-23. https://doi.org/10.1016/j.comptc.2019.01.022
- De la Garza, C. G. V., Narváez, W. E. V., Rodríguez, L. D. S., Fomine, S. (2020). Electronic structure of hybrid pentaheptite carbon nanoflakes containing boron-nitrogen motifs. Journal of Molecular Modeling, 26(4): 72. https://doi.org/10.1007/s00894-020-4324-9
- De la Garza, C. G. V., Narváez, W. E. V., Rodríguez, L. D. S., Fomine, S. (2021). Novel 2D allotropic forms and nanoflakes of silicon, phosphorus, and germanium: a computational study. Journal of Molecular Modeling, 27(5): 142. https://doi.org/10.1007/s00894-021-04775-4
- De la Garza, C. G. V., Rodríguez, L. D. S., Fomine, S., Vallejo Narváez, W. E. (2021). In silico modeling: electronic properties of phosphorene monoflakes and biflakes substituted with Al, Si, and S heteroatoms. Journal of Molecular Modeling, 27(6): 171. https://doi.org/10.1007/s00894-021-04789-y
- Enyashin, A. N., Ivanovskii, A. L. (2011). Graphene allotropes. Physica Status Solidi (b), 248(8): 1879-1883. https://doi.org/10.1002/pssb.201046583
- Grimme, S., Antony, J., Ehrlich, S., Krieg, H. (2010). A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. The Journal of Chemical Physics, 132(15): 154104. https://doi.org/10.1063/1.3382344
- Hättig, C. (2003). Geometry optimizations with the coupled-cluster model CC2 using the resolution-of-the-identity approximation. The Journal of Chemical Physics, 118(17): 7751-7761. https://doi.org/10.1063/1.1564061
- Hegarty, D., Robb, M. A. (1979). Application of unitary group methods to configuration interaction calculations. Molecular Physics, 38(6). https://doi.org/10.1080/00268977900102871
- Joensen, P., Frindt, R. F., Morrison, S. R. (1986). Single-layer MoS2. Materials Research Bulletin, 21(4): 457-461. https://doi.org/10.1016/0025-5408(86)90011-5
- Liu, H., Neal, A. T., Zhu, Z., Luo, Z., Xu, X., Tománek, D., Ye, P. D. (2014). Phosphorene: An unexplored 2D semiconductor with a high hole mobility. ACS Nano, 8(4): 4033-4041. https://doi.org/10.1021/nn501226z
- Narváez, W. E. V., Rodríguez, L. D. S., De la Garza, C. G. V., Fomina, L., Fomine, S. (2020). The electronic structure of Van der Waals heterostructures formed by the nanoflakes of black phosphorene with those of graphene and haeckelites: their complexes with Li. Journal of Molecular Modeling, 26(8): 204. https://doi.org/10.1007/s00894-020-04463-9
- Novoselov, K. S., Geim, A. K., Morozov, S. V., Jiang, D., Zhang, Y., Dubonos, S. V., Grigorieva, I. V., Firsov, A. A. (2004). Electric field effect in atomically thin carbon films.Science, 306(5696): 666-669. https://doi.org/10.1126/science.1102896
- Olmeda, E. M., Vera, C. G., Fomine, S. (2018). Electronic structure of phosphorene nanoflakes. A theoretical insight. Computational and Theoretical Chemistry, 1130: 33-45. https://doi.org/10.1016/j.comptc.2018.03.007
- Olmedo, E. M., De la Garza, C. G. V., Fomine, S. (2019). Modeling of silicon- and aluminum-doped phosphorene nanoflakes. Journal of Molecular Modeling, 25(9): 292. https://doi.org/10.1007/s00894-019-4182-5
- Ovchinnikov, A. A. (1978). Multiplicity of the ground state of large alternant organic molecules with conjugated bonds. Theoretica Chimica Acta, 47(4): 297-304. https://doi.org/10.1007/BF00549259
- Pablo-Pedro, R., López-Ríos, H., Fomine, S., Dresselhaus, M. S. (2017). Detection of multiconfigurational states of hydrogen-passivated silicene nanoclusters. The Journal of Physical Chemistry Letters, 8(3): 615-620. https://doi.org/10.1021/acs.jpclett.6b02773
- Pablo-Pedro, R., López-Ríos, H., Mendoza-Cortés, J.-L., Kong, J., Fomine, S., Van Voorhis, T., Dresselhaus, M. S. (2018). Exploring low internal reorganization energies for silicene nanoclusters. Physical Review Applied, 9(5): 054012. https://doi.org/10.1103/PhysRevApplied.9.054012
- Torres, A. E., Flores, R., Fomina, L., Fomine, S. (2016). Electronic structure of boron-doped finite graphene sheets: unrestricted DFT and complete active space calculations. Molecular Simulation, 42(18): 1512-1518. https://doi.org/10.1080/08927022.2016.1214955
- Torres, A. E., Flores, R., Fomine, S. (2016). A comparative study of one and two dimensional π-conjugated systems. Synthetic Metals, 213: 78-87. https://doi.org/10.1016/j.synthmet.2016.01.005
- Torres, A. E., Fomine, S. (2015). Electronic structure of graphene nanoribbons doped with nitrogen atoms: a theoretical insight. Physical Chemistry Chemical Physics, 17(16): 10608-10614. https://doi.org/10.1039/C5CP00227C
- Torres, A. E., Guadarrama, P., Fomine, S. (2014). Multiconfigurational character of the ground states of polycyclic aromatic hydrocarbons. A systematic study. Journal of Molecular Modeling, 20(5): 2208. https://doi.org/10.1007/s00894-014-2208-6
- Zade, S. S., Zamoshchik, N., Bendikov, M. (2011). From short conjugated oligomers to conjugated polymers. Lessons from studies on long conjugated oligomers. Accounts of Chemical Research, 44(1): 14-24. https://doi.org/10.1021/ar1000555
- Zhang, Y., Xu, X., Goddard, W. A. (2009). Doubly hybrid density functional for accurate descriptions of nonbond interactions, thermochemistry, and thermochemical kinetics. Proceedings of the National Academy of Sciences, 106(13). https://doi.org/10.1073/pnas.0901093106