www.mundonano.unam.mx | Mundo Nano| 2(1), enero-junio, 2009

Artículos de investigación

 

Procesos cuánticos en islas semiconductoras: manipulación óptica y control de estados coherentes

J. Enrique Rolón*

Sergio E. Ulloa*

* Department of Physics and Astronomy and Nanoscale and Quantum Phenomena Institute, Ohio University, Athens, Ohio 45701-2979, USA. 4 Junio 2009.

Introducción

Es notable que muchos de los avances científicos recientes y más asombrosos de nuestra sociedad, tanto en las ciencias físicas y químicas, como en las matemáticas mismas, derivan directamente de una de las leyes más peculiares de la naturaleza, la mecánica cuántica. A más de 100 años de su formulación, por algunas de las figuras más destacadas de la física de todos los tiempos, la mecánica cuántica sigue iluminando y causando perplejidad tanto en aficionados y estudiantes universitarios, como en expertos en las teorías más sofisticadas de la física (Tegmark y Wheeler, 2001). Lo que es quizá menos obvio, y que con frecuencia la sociedad en general ignora, es que muchos de los artefactos tecnológicos de uso común hoy en día, como el computador personal, el teléfono móvil, la televisión, la electrónica de aparatos electrodomésticos y la más avanzada instrumentación médica, existen gracias al entendimiento profundo de la naturaleza vía la física cuántica. Asimismo, el hombre ha buscado desde tiempo ancestral la forma de manipular la materia de tal manera que ésta exhiba propiedades físicas y químicas que no existen naturalmente. La química y la física han dirigido estos esfuerzos desde el advenimiento de la ciencia moderna. A lo largo de este camino, un reto actual es el de crear nuevos métodos para crear estructuras artificiales a escalas mucho más pequeñas que la escala macroscópica, pero grandes en comparación con los átomos mismos. Este reto tiene como objetivo obtener una nueva gama de materiales (y dispositivos construidos a partir de ellos) explotando las propiedades cuánticas de la nanoescala, con dimensiones de decenas o centenas de mil-millonésimas de metro (o 10-9 m= 1 nanometro). En efecto, esto ha sido posible en los últimos años, creando en el laboratorio estructuras materiales con propiedades fantásticas, pero completamente controladas o anticipadas gracias a la mecánica cuántica. Es en este contexto, presentamos algunos de los últimos desarrollos en las propiedades ópticas de los llamados puntos cuánticos en semiconductores. Estas técnicas nos permiten explorar el mundo nanoscópico al nivel de una sola “molécula” o “átomo” artificial, fabricado con puntos cuánticos.

La naturaleza a la nanoescala Posee una identidad doble

La mecánica cuántica predice que la materia a escala nanométrica (o escalas más pequeñas) revela su verdadera naturaleza dual, que incluye comportamiento como entes discretos o partículas, al mismo tiempo que muestra una naturaleza ondulatoria. Por ejemplo, un electrón, además de poseer momento mecánico p, p=mv, donde m es la masa del electrón y v su velocidad, tiene asociado una descripción ondulatoria caracterizada por una longitud de onda, l, (Resnik, 2002) . Esto implica que si uno hace pasar un electrón por una rendija de dimensiones comparables con l, éste sufre el fenómeno de difracción, al igual que en el caso de una onda luminosa. Además, las ondas de materia pueden interferir entre sí y cuando se habla de propiedades que pueden ser medidas en un experimento, es imprescindible considerar la naturaleza ondulatoria y hablar de la probabilidad de que dichas propiedades adquieran tal o cual valor. Por ejemplo, cuando uno considera una nube de electrones «orbitando» en un átomo (orbital ), no es posible decir dónde está el electrón a un determinado tiempo, sino sólo dónde es probable que se encuentre y dar dicha probabilidad. Más aún, no se pueden determinar simultáneamente su momento p y su posición con exactitud arbitraria. Para maravilla de unos y pesar de otros, esto ha sido comprobado experimentalmente repetidas veces en el siglo pasado.

La naturaleza ondulatoria y probabilística de las partículas cuánticas da también lugar a un fenómeno muy peculiar, el efecto de tunelaje cuántico, con el que es posible explicar desde los enlaces químicos entre átomos hasta fenómenos como el decaimiento espontáneo de los elementos radiactivos. De hecho, el tunelaje de electrones determina la operación de muchos de los dispositivos electrónicos modernos. Más recientemente, se han desarrollado microscopios capaces de observar objetos con resolución a escalas atómicas, que utilizan el efecto de tunelaje de electrones.

Nanoestructuras

A partir de la invención del transistor y los circuitos integrados, la física de semiconductores ha progresado enormemente en el desarrollo de dispositivos electrónicos de dimensiones reducidas, que rápidamente se han acercado más y más a tamaños nanométricos. Este esquema de miniaturización no puede continuar de manera arbitraria; sin embargo, debido a que cuando se alcance esta escala, el funcionamiento de dispositivos será fuertemente afectado por la mecánica cuántica (Wang, 2008), en formas que no se han incluido todavía en el diseño. Además de tratar de anticipar los problemas que la física cuántica introduzca en dispositivos en un futuro inmediato, una de las preguntas básicas actuales explora los tipos de dispositivos o nanoestructuras que pueden ser creados con nuevas funcionalidades gracias a efectos cuánticos. Una de estas alternativas interesantes es la construcción de los denominados puntos cuánticos y arreglos regulares conteniendo varios de éstos (veáse Figura 1).

 

Figura 1. a) Nube electrónica envolviendo un átomo aislado; b) dos (o más) átomos se combinan para formar una molécula mediante una redistribución de sus orbitales; c) arreglo periódico de moléculas forman un sólido cristalino; d) nanoestructura compuesta por una isla piramidal entre varias capas de redes cristalinas distintas, estas pirámides se “auto-ensamblan” en procesos controlados de crecimiento en superficies. (Figura realizada por Patrick Briddon, School of Electrical, Electronic & Computer Engineering).

 

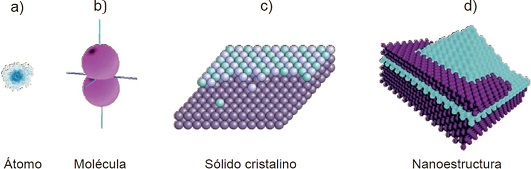
Los puntos cuánticos son objetos diseñados típicamente en semiconductores con el propósito de confinar electrones en las tres dimensiones espaciales, de modo de confinarlos a ‘cajas’ o volúmenes con dimensiones de sólo unos cuantos nanómetros (Wolverton, 2009). Es interesante observar que el electrón confinado exhibe propiedades cualitativamente similares a los electrones ligados a un átomo, aunque con otras energías y dimensiones características. Por ejemplo, el electrón en un punto cuántico tiene valores discretos de la energía bien definidos, asociados con el tamaño reducido del punto y que en términos generales corresponderían a diferentes orbitales en un átomo. De esta forma, a los puntos cuánticos también se les conoce como átomos artificiales (Leutwyler, 2001). Es de notar, sin embargo, que los niveles cuánticos en esos sistemas están separados por decenas de mili-electrón-Volts (en contraste con las decenas de electrón-Volts en un átomo natural), de modo que hay una gran diferencia no sólo en los tamaños sino en las escalas de energía de estos sistemas.

La gran ventaja de estos átomos artificiales es que pueden manipularse en un ambiente sumamente controlado de laboratorio, gracias a ser de mayor tamaño que los átomos ordinarios y a las diferentes técnicas de fabricación. Más aún, cambiando su geometría y composición química detallada, puede alterarse la estructura de niveles intrínsecos de la estructura y, por consiguiente, todas las propiedades espectroscópicas del punto cuántico.

Óptica cuántica en puntos cuánticos

Una de las ramas de la física atómica moderna es la óptica cuántica, que ha permitido investigar la respuesta óptica de los átomos al ser irradiados por campos electromagnéticos (luz) bajo diversas condiciones, las cuales incluyen la aplicación simultánea de campos eléctricos y/o magnéticos. En términos un poco más específicos, la óptica cuántica estudia fenómenos asociados con la luz misma como un ente cuantizado, es decir, cuando a la luz se le considera compuesta por corpúsculos luminosos en vez de un campo clásico descrito por intensidades. Los celebrados corpúsculos o fotones poseen cada uno una energía E = hn, donde h es la constante de Planck y n es la frecuencia (color) de la luz. Un haz de luz ‘clásica’, por cierto, contiene un número enorme de fotones. Uno de los efectos más conocidos en óptica cuántica, es el efecto de amplificación de luz por emisión estimulada de radiación o efecto láser por sus siglas en inglés, en donde la luz es emitida coherentemente por un medio que ha sido típicamente excitado óptica o eléctricamente.

El estudio de nanoestructuras, incluyendo sistemas de agregados de puntos cuánticos, combina los conocimientos de la física del estado sólido, la óptica cuántica y la física atómica, dando como resultado la posibilidad de alcanzar un nivel de miniaturización de componentes electrónicos donde los efectos cuánticos juegan un papel esencial y donde la materia exhibe nuevas propiedades controlables en experimentos.

Átomos y moléculas de dos niveles

Para entender la interrelación entre luz y materia en estos sistemas, partamos de la siguiente premisa básica. Los estados energéticos permitidos a un electrón orbitando en un átomo toman valores discretos; por simplificación, consideremos que posee dos estados, E1 y E2, donde el primero es el estado de más baja energía. Cuando un átomo es irradiado por luz, éste puede absorber un fotón y sufrir una transición (excitación) adquiriendo la energía del fotón para llevar al electrón desde el estado de baja energía E1 al estado de más alta energía, E2. Este proceso requiere que la energía del fotón incidente sea igual a la diferencia energética entre los niveles atómicos, esto es, hn = E2 -E1 (Figura 2). El proceso inverso también es posible, tal que un electrón en un estado excitado con energía E2 se relajaría al estado E1emitiendo un fotón de frecuencia n = (E2-E1)/h.

 

Figura 2. Creación de un exciton por bombeo óptico. Un fotón de energía hn es absorbido en el punto cuántico, promoviendo un electrón de su estado base a la banda de conducción que deja hueco en la banda de valencia. Este proceso se puede interpretar como la creación de un exciton |X〉 desde el estado “vacío” |0〉, en donde no hay excitones y todos los electrones ocupan completamente la banda de valencia.

 

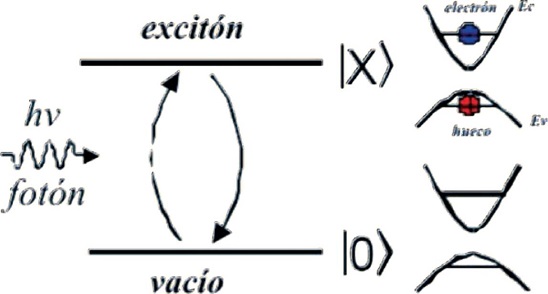
Ahora, cuando dos átomos se combinan para formar una molécula, ésta poseerá también una estructura de niveles. En un sólido, conformado por millones de átomos, esta descripción sufre una modificación importante. Dado el enorme número de átomos en el sólido, éstos poseen un número también enorme de niveles energéticos, cuya separación entre ellos es tan pequeña, que las posibles energías de transición forman un cuasi continuo de valores (denominadas bandas de energía), separadas típicamente a su vez de otras bandas por valores en donde las transiciones no son posibles (bandas prohibidas). En sólidos semiconductores, los miles de millones de electrones ocupan totalmente un número de bandas energéticas (de las cuales la de más alta energía es la banda de valencia), dejando otras completamente vacías y separadas entre sí por una ‘brecha’ de energía (o gap, por su término en inglés) de un tamaño característico al material semiconductor usado (que, por supuesto, depende de la composición química detallada).

Esta configuración energética resulta en una situación interesante. Cuando el material semiconductor es irradiado por luz de energía (frecuencia) mayor al gap en cuestión, fotones son absorbidos, llevando a los electrones a ocupar la banda ‘vacía’ superior (llamada de conducción). En este fenómeno de absorción de luz, un electrón es promovido a la banda superior, mientras que deja detrás una vacancia (o hueco) en la otrora-llena banda inferior de valencia.

Excitones

Cada vez que un electrón es excitado y un hueco es creado en la banda inferior, sucede un fenómeno interesante que parece ser relativamente simple, pero está lleno de sutilezas. Resulta que como hay otros electrones ocupando la banda inferior, el electrón promovido por el fotón deja un ‘lugar’ que puede ser ocupado por otro electrón de esta banda, este último deja otro hueco que, a su vez, puede ser ocupado por otro electrón,y así sucesivamente . De esta manera, se puede pensar que cada hueco en la banda inferior se comporta como una partícula que se mueve en dirección opuesta a los electrones y que como tal tiene una carga efectiva positiva. El movimiento de estos huecos (o agujeros) genera una corriente opuesta a la del electrón. Más interesante aún, estas partículas con carga positiva efectiva son atraídas a los electrones, que bajo condiciones adecuadas pueden formar un estado ligado semejante al que un electrón en un átomo común y corriente tiene cuando se liga al núcleo positivo. A este par ligado de electrón-hueco se le llama excitón (Lundstrom et al., 1999) , véase la Figura 2, y puede pensarse como una cuasi-partícula neutra compuesta y sujeta a interaccionar con otros electrones, huecos, iones u otros excitones presentes; además de ser capaz de transportarse de un lugar a otro dentro del semiconductor. A este objeto nanoscópico se le puede también asociar una energía y correspondiente función de onda para su descripción cuántica. Sin embargo, es importante no olvidar que el electrón mismo está en un estado excitado, de modo que después de un tiempo característico, llamado vida media del excitón, éste se recombina, regresando hacia la banda de valencia y destruyendo al excitón por completo. Al desaparecer el excitón de esta manera, se genera un fotón con una frecuencia característica del material. Es así, de hecho, como se genera la luminiscencia típica en un fotodiodo (led), donde éste emite en la región visible del espectro electromagnético (aunque otras frecuencias son posibles para los led). Curiosamente, por un proceso físico similar es que las luciérnagas y algunos animales en los abismos del mar emiten luz, aunque claro que ahí los excitones son generados en biomoléculas localizadas en las células del tejido de estos seres.

Si seguimos esta línea de razonamiento, puede pensarse en la posibilidad de generar excitones con estructuras más complicadas, y de hecho así es. Existen excitones neutros llamados biexcitones, compuestos por dos electrones y dos agujeros que residen en cercana proximidad en el sólido. Otros excitones con carga residual neta, llamados triones, consisten en dos electrones (o huecos) más un hueco (o electrón), conformando triones negativos (o positivos). Otras combinaciones son posibles en principio; sin embargo, entre más electrones o huecos posean estos complejos, más inestables son y más corta es su vida media.

Excitones en puntos cuánticos y moléculas artificiales

En un punto cuántico, las funciones de onda tanto de un electrón como de un hueco están confinadas en un espacio muy reducido (del orden de la longitud de onda característica de las partículas). Al crearse un excitón en el punto cuántico, el electrón-hueco que lo compone se liga fuertemente formando un excitón confinado. Similarmente, al recombinarse el excitón se produce fotoluminiscencia provenientemente de una región localizada en el espacio. El grado de confinamiento que produce un punto cuántico ofrece la posibilidad de que las energías de los diferentes excitones que pueden ser foto-generados exhiban una cuantización adicional, al igual que los electrones por sí mismos. Un punto cuántico, entonces, puede verse como un átomo artificial compuesto por electrones, huecos y excitones. Desde luego, hay muchas otras propiedades de los puntos cuánticos que tienen análogos en otros objetos cuánticos, pero lo que nos interesa aquí es la analogía atómica y molecular. De modo que la pregunta natural concierne al espectro excitónico que pudiera exhibir un punto o molécula cuántica artificial (Stinaff et al., 2006). ¿Qué ventajas y posibles aplicaciones ofrecen la física de excitones en estas nano estructuras? Una respuesta interesante surge cuando consideramos complejos estructurales que involucran múltiples puntos cuánticos. De éstos, los pares de puntos acoplados son considerados de particular importancia.

Nanofabricación de moléculas artificiales

Consideremos el caso de dos puntos cuánticos auto ensamblados, fabricados en el laboratorio por una técnica de crecimiento de superficies por epitaxia de haces moleculares, (Tsao, 1993) llamada de Stranski-Krastanov. Mediante esta técnica, es posible crecer una superficie en un sustrato dentro de una cámara de alto vacío, a través del bombardeo controlado del sustrato cristalino con diferentes haces de moléculas o átomos de la especie química deseada. A medida que la primera capa de material se forma sobre el sustrato, ésta se arregla en una estructura cristalina, siguiendo la estructura dictada por el sustrato. Sin embargo, cuando el espaciamiento entre los átomos del sustrato es sustancialmente diferente al de los átomos formando la capa, la aleación que se forja entre éstas dos es sujeta a fuerzas de estrés a medida que los átomos de capa y sustrato tratan de encontrar su periodicidad ideal. Este estrés generado en la red se minimiza con la formación de islas de dimensiones nanométricas, puntos cuánticos, como se aprecia en la Figura 3a. Estas islas pueden adquirir diferentes geometrías, como pirámides truncadas, cilindros truncados, o secciones elípticas, dependiendo de las condiciones de crecimiento, véase la Figura 3c. Asimismo, es posible crecer sobre estas islas una capa del mismo material del sustrato, repetir el proceso y generar una capa de islas encima. En este caso, los mismos esfuerzos que producen las islas favorecen la formación de pares de islas una sobre la otra, véase la Figura 3b. Ahora, si el material del sustrato posee un gap mayor entre sus bandas de conducción y valencia que en el material que constituye al punto cuántico, es posible que el punto cuántico resulte efectivamente como un pozo energético de potencial. En este caso, el sustrato resulta ser como una barrera a los electrones que residen en el punto, pues les resultaría difícil excitarse hacia la banda de conducción del sustrato. De manera inversa, los electrones que viven en el sustrato ven al punto cuántico como un pozo en donde podrían relajarse a niveles más bajos de energía. Esta situación la podemos apreciar en la Figura 4, donde un par de puntos cuánticos produce un par de pozos de potencial en la banda de conducción.

 

Figura 3. a) Crecimiento epitaxial de puntos cuánticos en forma de islas; b) micrografía por microscopía electrónica de transmisión de un par de puntos cuánticos auto ensamblados, creación de una molécula artificial efectiva para los electrones y huecos; c) acercamiento de un solo punto cuántico. (Figura realizada por T.L Reinecke y D. Gammon, Naval Research Laboratory , Washington DC, EUA).

 
 

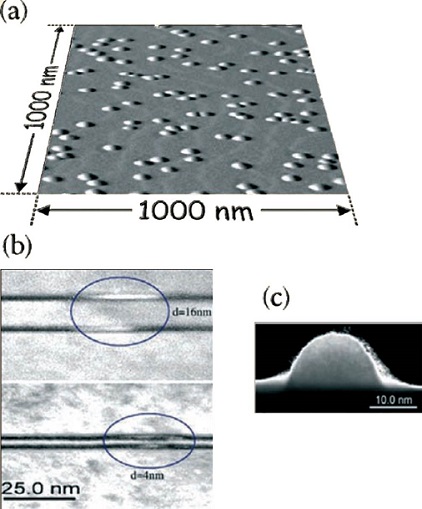
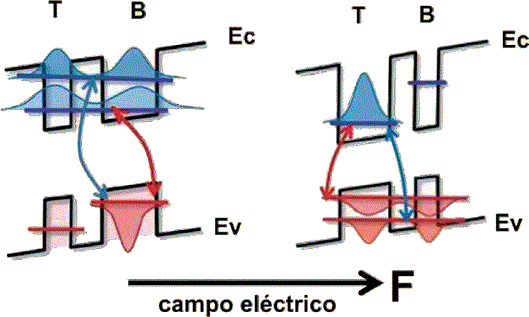
Figura 4. Diagramas de banda de energía de una molécula de puntos cuánticos T y B. Banda de conducción Ec y de valencia Ev, en presencia de un campo eléctrico F. (Panel izquierdo) Los niveles de energía del electrón de T y B en resonancia promoviendo el traslape de sus funciones de onda o tunelaje del electrón. (Panel derecho) Niveles del agujero en resonancia, promoviendo tunelaje del agujero. (Figura realizada por G. Abstreiter y J.J. Finley, Walter Schottki Institut, Technische Universität München, Am Coulombwall 3, D-85748 Garching, Germany).

 

Moléculas artificiales: transferencia Förster de energía y tunelaje cuántico

Uno se pregunta ¿qué tipo de interacciones ocurren en un par de dos puntos cuánticos? Hablamos anteriormente del efecto de tunelaje como uno de los principales responsables del acoplamiento entre puntos cuánticos cercanos. Para entender cómo opera en esta nanoestructura, recordemos que los puntos cuánticos están separados por un material que funge como una barrera de potencial, la cual aumenta con el espesor de dicho material. Así, cuando un excitón es generado en uno de los puntos, tanto el electrón o el hueco que lo constituye pueden realizar un tunelaje cuántico hacia el otro punto. De esta forma si uno calculara la probabilidad de encontrar al electrón o al agujero en cierto lugar del espacio, encontraríamos que la probabilidad se distribuye en una región extendida entre los dos puntos cuánticos. De esta forma el electrón (hueco) está descrito por una nube electrónica (distribución de carga) no localizada en un solo punto. Si recordamos un poco de química, resulta que ésta es la manera de representar cuánticamente los enlaces químicos entre dos átomos, donde una nube electrónica es compartida entre ellos, siendo la intensidad de dicho enlace dependiente de la geometría de la nube. Es así que dos puntos cuánticos acoplados por tunelaje dan origen a una molécula artificial. Esto lo podemos observar en más detalle en la Figura 4, en donde dos puntos cuánticos T y B, en presencia de un campo eléctrico, pueden acoplarse por tunelaje del electrón o del hueco, dependiendo del valor del campo aplicado. El campo eléctrico sintoniza en o fuera de resonancia los niveles respectivos del electrón y el agujero en ambos puntos, promoviendo un mayor traslape de las funciones de onda y efectivamente cambiando la naturaleza del enlace químico de esta molécula artificial: sabemos que cuando dos o más estados se acoplan entre sí, éstos forman una mezcla tal que sus funciones de onda se combinan y dan lugar a nuevos estados cuánticos y a posibles efectos de interferencia. Estas mezclas afectan de manera directa la probabilidad de encontrar los electrones o huecos de los excitones en una región particular de la molécula. En el lenguaje molecular ortodoxo, se dice que la molécula artificial adquiere diferentes tipos de enlace, caracterizados por la geometría de las nubes electrónicas compartidas de sus componentes. Si el tunelaje entre las moléculas es fuerte, las nubes electrónicas del electrón (hueco) se distribuyen en forma extendida a lo largo de ambos puntos cuánticos, con una probabilidad alta de encontrarse en la barrera entre ellos y dando lugar a un traslape fuerte entre las dos funciones de onda. En contraste, si el traslape entre estas funciones de onda es débil, se espera el confinamiento de la nube electrónica a un solo punto cuántico. En el primer caso, se dice que los puntos se acoplan (enlazan) fuertemente, mientras que en el otro se acoplan débilmente por tunelaje.

Dado que en un punto cuántico viven partículas cargadas (electrones y huecos), las interacciones tanto estáticas como dinámicas juegan un papel importante en los mecanismos de acoplamiento molecular. Una de las particularidades de la interacción de Coulomb es que es de largo alcance, decayendo inversamente proporcional a la distancia entre la separación de las cargas. La variación con la distancia entre objetos con distribuciones de carga de geometrías más complicadas puede ser diferente. Por ejemplo, en el caso de dipolos eléctricos formados entre pares neutros de electrónhueco en un excitón, la interacción varía como el inverso de la distancia al cubo. En efecto, cuando dos excitones son fotogenerados en diferentes puntos cuánticos de la molécula, cada uno de ellos representando un dipolo, éstos interaccionan vía la interacción dipolo-dipolo que varía inversamente proporcional al cubo de la distancia entre ellos.

Es interesante observar que la interacción dipolo-dipolo da lugar a un efecto más sutil que resulta en la transferencia de excitación óptica desde un punto cuántico al otro. Imaginemos que es posible excitar continuamente un solo punto cuántico con un láser, esta excitación genera un proceso dinámico mediante el cual se crean y destruyen excitones. Esta energía producida por la excitación en un punto cuántico puede en efecto ser transferida al punto vecino, provocando en él la creación de un excitón secundario. Este proceso es llamado transferencia Förster de energía (Orrit, 1999), y es un mecanismo que ocurre de manera natural en muchos procesos biológicos, involucrando la transformación de energía luminosa en otras formas de energía, dando lugar a muchas reacciones bioquímicas. Cabe mencionar que hoy en día se buscan crear dispositivos híbridos a base de nanoestructuras semiconductoras y biomoléculas orgánicas que toman ventaja de este mecanismo (Shimon, 1999).

Signaturas ópticas y control de moléculas artificiales

Surge ahora la pregunta final en este relato. ¿Qué propiedades podrían identificarse en moléculas artificiales acopladas por tunelaje y transferencia de Förster? Para ello puede pensarse en un modelo. Imaginemos que dos puntos acoplados son colocados dentro de un dispositivo (chip) electrónico e irradiados por luz láser, véase Figura 5. El chip además puede proveer a los puntos con un campo eléctrico externo que tendría el efecto de modificar la geometría de las nubes electrónicas asociadas a los electrones y huecos de los excitones, como hemos descrito arriba (Krenner et al., 2005). A su vez, el láser puede adquirir diferentes frecuencias e intensidades luminosas, permitiendo acceder a diferentes niveles de energía de la molécula artificial y sus correspondientes estados excitónicos, los cuales son los más relevantes para fines de nuestra discusión. Así, tenemos dos parámetros de control de los estados cuánticos. Si la luz láser ilumina continuamente el chip, podríamos pensar que un haz de fotones inunda la molécula, de modo que cualquier cambio o transición excitónica en uno de los puntos cuánticos, afectaría el campo de radiación inmediato. En este efecto sobre los estados energéticos de la molécula se dice que son vestidos por el campo de radiación. De hecho, es la combinación de estos estados vestidos la que describe la naturaleza de las diferentes configuraciones posibles de la molécula artificial así como la evolución temporal del estado cuántico bajo diferentes condiciones experimentales externas.

 

Figura 5. (Panel izquierdo) Molécula artificial de arseniuro de indio (InAs), crecida sobre un sustrato de arseniuro de galio (GaAs). Punto cuántico T es crecido directamente sobre el punto B, separados por una distancia d. (Panel derecho) Un ensamble de moléculas es embebido en un chip de Schottky proveyendo un campo eléctrico F. A pesar de la presencia de otras moléculas vecinas, una sola molécula es seleccionada por excitación óptica por luz láser, gracias a una máscara con perforaciones en la parte superior del chip (Krenner et al., 2005)

 

Cuando la molécula no es excitada, podríamos pensar que su estado está caracterizado por el vacío, o ausencia de excitones. Y cuando lo es, la molécula es ocupada por diferentes especies de ellos (excitones neutros, biexcitones, triones, entre otros). Como se mencionó anteriormente, estos excitones se acoplan simultáneamente por tunelaje y acoplamiento Förster.

La naturaleza de los orbitales de la molécula artificial caracteriza a su vez la naturaleza de los excitones que pueden ocurrir en la molécula. Por ejemplo, si es sólo el electrón que se extiende entre los dos puntos, mientras que el hueco queda confinado en uno de ellos, en un límite se puede hablar de un excitón indirecto, en donde el electrón y el hueco están en diferentes puntos de la molécula. Por otro lado, cuando ambos, electrón y hueco, se localizan en el mismo punto, hablamos de un excitón directo. Lo mismo ocurre para biexcitones, habiendo biexcitones directos (con dos electrones y dos huecos en el mismo punto), así como un biexcitón indirecto puede descomponerse en un electrón extendido entre dos puntos y un trión localizado en el otro.

De esta manera, podemos etiquetar cada uno de los excitones con el símbolo 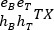donde los superíndices eB y eT denotan que un gran porcentaje de la nube de probabilidad del electrón está localizada en el punto cuántico B y T, respectivamente, y de manera análoga para los subíndices del hueco hB y hT. Así, por ejemplo, 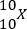sería un excitón con carácter directo en el punto B mientras que 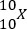sería un excitón con carácter indirecto con un electrón en B y un agujero en T. El bombeo de un excitón directo en el punto B sería representado por 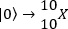, donde |0〉 es el estado vacío en la molécula; similarmente, un proceso de tunelaje del electrón a partir del excitón directo en el punto 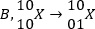, produce un excitón indirecto y así sucesivamente.

Ahora, lo que realmente define en última instancia la naturaleza de los enlaces moleculares y ejemplifica las fantásticas habilidades experimentales modernas es el comportamiento dinámico de las funciones de onda excitónicas, que pueden ser finamente controladas en el laboratorio al nivel de una sola molécula. Este control resulta en efectos de interferencia interesantes que dan lugar a probabilidades dependientes del tiempo, donde un valor máximo de la probabilidad corresponde a una interferencia constructiva de estas ondas y ocupación máxima de un estado excitónico en particular. Bajo condiciones experimentales adecuadas, la dinámica de las probabilidades de ocupación de estados exhibe un comportamiento oscilatorio regular, llamadas oscilaciones de Rabí, en donde un sistema de dos niveles simples, por ejemplo, es controlado por la radiación incidente resonante. En particular, la amplitud de estas oscilaciones es controlada directamente por la diferencia de energía entre la frecuencia del láser y la energía de creación mínima del nivel excitónico. La amplitud de oscilación es pequeña cuando esta diferencia de energías es muy grande (y el láser se dice está muy fuera de tono con el nivel en cuestión), pero crece cuando las dos energías son iguales (y el láser está en resonancia).

En el laboratorio, se tienen entonces una serie de controles finos sobre el estado cuántico de la molécula. Por una parte, el campo eléctrico externo deforma los orbitales de la molécula, haciendo el tunelaje cuántico de los electrones o huecos más o menos difícil (y por ende cambiando el traslape de las funciones de onda asociadas y la naturaleza del enlace). Por otra parte, la frecuencia del láser que se usa para crear los excitones puede acercarse a una condición resonante, modificando las poblaciones de los diferentes excitones en una forma dinámica. Finalmente, la molécula puede ser “interrogada” monitoreando la luz que es emitida por la molécula, completando el ciclo de definición-control-interrogación del sistema cuántico molecular de puntos semiconductores.

En este amplio contexto con potencial para afectar el comportamiento cuántico de dichos objetos nanoscópicos, cabe preguntar cuál es el efecto de la transferencia Förster de energía, cómo compite con los procesos de tunelaje y bombeo óptico, y cómo puede quizá utilizarse para mejorar más aún el control sobre estas moléculas. Justo esta pregunta hemos analizado con detalle en un trabajo reciente. (Rolón y Ulloa, 2009). Como se puede apreciar en las Figuras 6 y 7, el efecto Förster provoca el “desdoblamiento” de líneas espectrales (en donde dos líneas aparecen en vez de una sola, si por ejemplo comparamos los paneles a y b en la Figura 6), asociadas a los orbitales excitónicos de carácter directo, para campos eléctricos intensos, F > 80 kV/cm para el caso de las figuras. Vemos que a diferencia del tunelaje, que acopla excitones directos con indirectos (vía el tunelaje de electrones o huecos), la interacción de Förster acopla dos excitones directos como un todo. El desdoblamiento de las líneas excitónicas directas es análogo al desdoblamiento de las líneas espectrales atómicas por un campo magnético o eléctrico efectivo, como sucede en el efecto Zeeman o Stark, respectivamente. En nuestro contexto, el desdoblamiento se explica por el hecho de que la interacción de Förster afecta tanto los orbitales del agujero como los del hueco simultáneamente, provocando que el estado cuántico resultante sea una mezcla de las funciones de onda de estados excitónicos directos: diferencia del efecto del tunelaje, donde una de las partículas se deslocaliza entre los dos puntos, el desdoblamiento aquí se debe a la transferencia de excitación óptica y no a la deformación geométrica de los orbitales. Algo muy importante en este sistema es que el campo eléctrico promueve (o controla) que los niveles de energía de los dos puntos cuánticos entren en resonancia, favoreciendo tanto el fenómeno de tunelaje de cargas como el mecanismo de Förster. En la mayoría de las moléculas estudiadas en experimentos, el efecto del tunelaje que deforma el orbital para una sola de las partículas en cuestión, electrón o agujero, acaba por dominar sobre la mezcla causada por Förster, destruyéndola por completo. Esto se aprecia en la Figura 6, justo en la región del mapa alrededor de F=± 20 kV/cm, en donde la mezcla de los diferentes orbitales excitónicos es completa, produciendo poblaciones casi idénticas sobre una región amplia de campo. La repulsión de líneas espectrales observada ahí es debida esencialmente al acoplamiento cuántico por tunelaje, mientras que la mezcla por la interacción de Förster es sólo notable para campos grandes, como mencionamos antes.

 

Figura 6. a) Distribución de probabilidad de cada uno de los excitones presentes en la molécula artificial, en función del campo eléctrico aplicado F en unidades de kilo-voltios por centímetro y energía (frecuencia) de luz láser aplicado en unidades de mili-electrón voltios; b) el acoplamiento coherente de Förster promueve el desdoblamiento de las líneas excitónicas con carácter directo indicada por las flechas (Rolón y Ulloa, 2009).

 
 

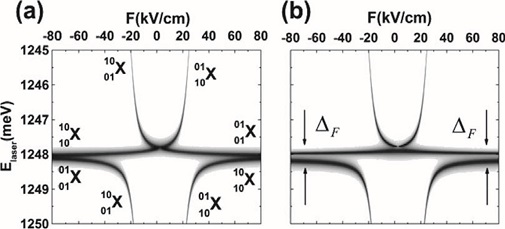
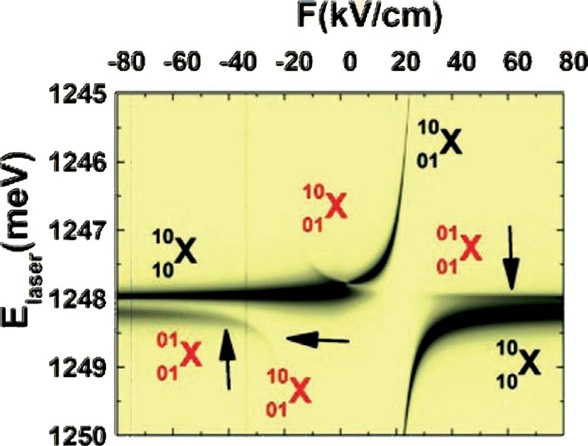
Figura 7. Distribución de probabilidad (población de niveles) correspondiente al excitón directo localizado en el punto B. Se observa que este excitón se mezcla con otros tipos de excitones (distintas hibridaciones orbitales) dependiendo del valor del campo eléctrico y de la energía de láser de bombeo. En rojo se observa la mezcla simultáneamente con el excitón directo en el punto T y un excitón indirecto. La flecha de la esquina inferior izquierda muestra el correspondiente desdoblamiento de esta mezcla por acoplamiento Förster (Rolón y Ulloa, 2009).

 

Es esta variación controlada de parámetros externos capaces de acoplar y desacoplar los puntos cuánticos lo que hace a estas nanoestructuras sumamente atractivas. Una aplicación que está en la frontera de la investigación en todo el mundo es la de hacer que éstas moléculas funcionen como un interruptor lógico cuántico, o bit cuántico (qubit es el término usado en inglés). Posibles qubit lógicos en este sistema molecular serían la presencia (o ausencia) de un excitón en un punto, la presencia (ausencia) de un electrón o agujero en un punto u otro, o cualquier otra configuración bipartita de la molécula artificial. Las posibles operaciones cuánticas de este qubit deseables para implementar una computadora cuántica están limitadas por el grado de estabilidad de los excitones y de las conformaciones moleculares de ellos. Aunque los retos para llegar a esta meta son importantes, este campo sigue avanzando con la colaboración entre teóricos y experimentales. Además de lograr un mejor entendimiento de estos sistemas cuánticos y de ser capaces de controlarlos una-molécula-a-la-vez, ofrecen la promesa de nuevas aplicaciones como en computación e información cuántica. Otros ejemplos incluyen quizá la fabricación de materiales “inteligentes”, con la capacidad de responder a estímulos externos y exhibir propiedades completamente distintas, dependiendo del valor de los parámetros de control.

Bibliografía