www.mundonano.unam.mx | Mundo Nano| 2(1), enero-junio, 2009

Artículos de investigación

 

Grafeno: un paso hacia el futuro

E. Martínez-Guerra*,**

M. E. Cifuentes-Quintal*

R. De Coss*

* Departamento de Física Aplicada, Cinvestav-Mérida, Apdo. Postal 73, Cordemex 97310, Mérida, Yucatán, México.

** Facultad de Ciencias Físico-Matemáticas, UANL, Av. Universidad s/n. Cd. Universitaria 66451, San Nicolás de los Garza, Nuevo León, México.

Resumen:

Desde su descubrimiento en 2004, el grafeno ha generado una gran expectativa para sustituir la tecnología actual basada en silicio. En este trabajo, discutimos de manera simple cuáles son las propiedades que sustentan esta expectativa. En particular, nos referimos a las propiedades electrónicas y de transporte que se pueden aprovechar en dispositivos de alta velocidad. Además, presentamos una comparación (teoría y experimento) de las cantidades físicas que deben ser controladas antes de diseñar esta clase de dispositivos: dispersión de energía, velocidad de Fermi y masa ciclotrónica. Finalmente, proyectamos algunas formas de modular estas cantidades.

Importancia de divulgación. El grafeno es sin duda un material que revolucionará la tecnología actual. Sin embargo, a casi 5 años de su descubrimiento, en México hay muy pocos grupos de investigación que lo estudian en forma experimental y teórica. Estamos convencidos que es fundamental interesar a jóvenes de bachillerato y estudiantes universitarios en la investigación básica y aplicada de este material si queremos que nuestro país no se quede al margen de las próximas innovaciones tecnológicas, como ya le ocurrió a la generación del silicio.

 

Introducción

En marzo del 2007, asistimos a la reunión anual de la Sociedad Americana de Física, en Denver, EUA, y entre pasillos escuchamos que se había sintetizado un nuevo material llamado “grafeno” que, como el silicio, vendría a revolucionar la industria y la tecnología de nuestra generación. Preguntamos a quienes discutían sobre este descubrimiento, qué clase de material era éste y nos contestaron: “es simplemente una membrana de carbono del espesor de un átomo”. ¿Qué características volvían tan especial a esta membrana si está formada solamente de átomos carbono? La respuesta se encuentra en su estructura cristalina y baja dimensionalidad. Es conocido que el carbono tiene una gran capacidad para formar redes complejas con otros elementos, lo cual ha sido la base de la química orgánica y de la existencia de vida en nuestro planeta. Asimismo, se sabe que el carbono elemental forma una variedad de estructuras de distinta dimensionalidad desde las más estables como el diamante y el grafito (3D) descubiertas hace mucho tiempo hasta compuestos de baja dimensionalidad como los fulerenos (0D) (kroto et al., 1985) y los nanotubos (1D) (Ijima, 1991). En esta secuencia de dimensionalidad faltaba la estructura 2D, no obstante, a nadie le había interesado buscarla porque en los años treinta del siglo XX, Peierls (1934, 1935) y Landau (1937) habían demostrado teóricamente que este material era termodinámicamente inestable y no podía existir. Sin embargo, recientemente se ha podido sintetizar, y sus propiedades lo han convertido en el candidato ideal para sustituir la actual tecnología del silicio.

Historia

En estos tiempos, uno se imagina que los grandes descubrimientos sólo se realizan utilizando tecnología muy sofisticada, pero esto no siempre es así, éste fue el caso del grafeno. En 2004, Andre Geim, Kostya Novoselov y colaboradores colocaron, en la Universidad de Manchester, una cinta adhesiva sobre una muestra de grafito y la removieron consecutivamente hasta aislar una sola capa de átomos de carbono, poniendo fin a las predicciones de Pierls y Landau de que este material no podría aislarse sin que las vibraciones del material a temperatura ambiente lo destruyeran. Ahora es conocido que el material es estable, porque sus vibraciones se acomodan en ondulaciones con amplitudes de alrededor de 1 nanometro a lo largo de la membrana atómica (Carlsson, 2007; Fasolino et al. 2007; Geim y Novoselov, 2007) Estas ondulaciones son intrínsecas del grafeno y son resultado de inestabilidades vibracionales. En la Figura 1a, se muestra una imagen esquemática de la estructura de este material y en la 1b, su imagen tomada con un microscopio electrónico de barrido. Después de algunos meses de su descubrimiento, el grupo de Geim perfeccionó el método de síntesis original (Novoselov et al., 2005) sustituyendo la cinta adhesiva con una superficie dura donde se deslizaban muestras de grafito. Pocos meses después, Zhang, en la Universidad de Columbia, validaba que esta técnica era apropiada para sintetizar grafeno de manera reproducible (Figura 2) (Zhang et al., 2005) Al mismo tiempo, Walt de Heer y Claire Berger, en el Tecnológico de Georgia, desarrollaron un procedimiento de crecimiento “epitaxial” para producirlo a escala industrial (Heer et al., 2007). Así, a 4 años de su descubrimiento, se han desarrollado distintas técnicas de crecimiento tales como: depósito por vapores químicos, reducción de SiC, reducción de N2H4 y reducción de etanol con Na, los cuales permiten obtener muestras de mejor calidad que las técnicas originales.

 

Figura 1. a) Imagen esquemática a escala atómica del grafeno; b) imágenes de grafeno obtenidas con un microscopio electrónico de barrido (escala de micras).

 
 

Figura 2. a) Imagen de una muestra de grafito tomada con un microscopio electrónico de barrido (MEB); b) esquema del proceso de exfoliación del grafito para sintetizar grafeno; c) muestras de grafeno sobre un sustrato de SiO2 y, d) dispositivo experimental de grafeno con contactos de oro para medir sus propiedades de transporte (tomado de Zhang et al., 2004).

 

Propiedades

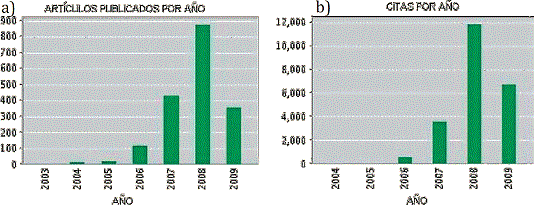
Desde su descubrimiento en 2004 a la fecha (27 mayo 2009), se han publicado 1,842 artículos científicos con arbitraje internacional, y cada año incrementa exponencialmente el número de citas dedicadas a entender las propiedades de este material (Figura 3), pero ¿por qué tanto interés en este material? Entre sus propiedades destacan: alta calidad cristalina (~1 defecto/mm2), portadores de carga (electrones y huecos) tipo fermiones de Dirac sin masa, alta movilidad de portadores de carga (15,000 cm2/ Vs a 300 K y 200,000 cm2/Vs a 4 K) y transporte balístico en la escala de 1 mm a temperatura ambiente. Pueden mencionarse otras, pero sin duda son estas propiedades electrónicas y de transporte las que han ocupado de manera importante el quehacer científico de los últimos años.

 

Figura 3. Reporte de: a) número de publicaciones y, b) citas anuales sobre grafeno (Fuente: Web of Science, 27 de mayo 2009).

 

Propiedades electrónicas

Los átomos poseen electrones que se encuentran cerca de sus núcleos, así como electrones lejos de ellos (de valencia). Los electrones de valencia logran separarse de los núcleos cuando reciben energía adicional externa. Por ejemplo, cuando se aplica un campo eléctrico a un material, estos electrones de valencia se separan de sus núcleos y se convierten en electrones de conducción. En el caso de materiales constituidos por átomos que no tienen sus capas electrónicas completas, existen huecos (ausencia de electrones en la banda de valencia) que también pueden separarse de los núcleos si se les adiciona energía. Ésta es la forma en que se producen corrientes de electrones o huecos en un semiconductor. Estos portadores de carga (electrones o huecos) de conducción colisionan entre sí, disminuyendo la velocidad a la que se mueven; sin embargo, en el grafeno, los electrones o huecos se comportan como partículas que se mueven a una velocidad constante, viajando distancias del orden de micras (1×10-6 m) sin sufrir dispersión. Este hecho determina que la movilidad de los electrones sea de alrededor de 200,000 cm2/Vs en comparación a los 140,000 cm2/Vs en el silicio y 77,000 cm2/Vs en la aleación In-Sb. Ésta es la característica más atractiva del grafeno. ¿Qué les permite moverse a los portadores de esa manera en el grafeno?, la respuesta se encuentra en su estructura electrónica, pues determina las energías características que pueden tener los portadores de carga en un material. En un material convencional, la relación de dispersión de energía de un electrón o hueco es del tipo parabólica/cuadrática, esto es:

 
 

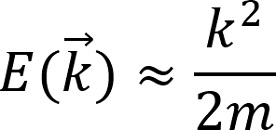
donde m es la masa efectiva del portador y k su momentum. Asimismo, la velocidad de un portador está descrita por:

 
 

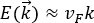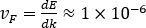de esta manera, la velocidad de un portador depende normalmente de la energía que adquiere como resultado de las interacciones colectivas. Sin embargo, en el grafeno, la relación de dispersión de la energía alrededor del nivel de Fermi (EF) es aproximadamente lineal, esto es: , donde νF es la velocidad de Fermi y, por lo tanto, νF es una constante: . Esta relación lineal, entre la energía y el momentum de los portadores, fue predicha teóricamente por Wallace hace muchos años (Wallace, 1947), y se confirmó muy recientemente en forma experimental (Bostwick et al., 2007). Bostwick y colaboradores emplearon la técnica de espectroscopía arpes (Angle Resolved Photo Electron Spectroscopy) para medir la función espectral de los portadores de carga en el grafeno (Figura 4a). También se han estudiado las propiedades electrónicas de este material, mediante metodologías numéricas basadas en el contexto de la Teoría del Funcional de la Densidad. En este sentido, la Figura 4c corresponde a la estructura de bandas obtenida por cálculos de primeros principios (Cifuentes-Quintal et al., s/f) y la Figura 4b es una vista tridimensional de 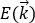dentro de la región circular del espectro teórico. Ambos espectros (teórico y experimental) coinciden, y la dispersión 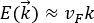define una superficie tridimensional llamada “conos de Dirac” por la geometría cónica que presentan y por la similitud al espectro de energías de fermiones de Dirac sin masa (Semenoff, 1987; Haldane, 1998).

 

Figura 4. Estructura de bandas del grafeno: a) espectro de energías experimental como función del momentum en las direcciones principales de la zona de Brillouin (tomado de Bostwick et al., 2006) b) acercamiento de la estructura de bandas calculada donde se observa la banda de valencia y de conducción (Conos de Dirac) y c) estructura de bandas calculada.

 

Ecuación de Dirac y Conos de Dirac

La ecuación de Dirac describe el comportamiento de partículas de espín ½ (fermiones), ej.: el electrón, cuando se mueve a velocidades cercanas a la luz (c), pero en el grafeno los portadores de carga se mueven a velocidades mucho más bajas (c/300), ¿cuál es entonces la conexión de estos portadores con la electrodinámica cuántica?

La ecuación de Dirac está sustentada en la mecánica cuántica y la teoría de la relatividad y una de las aportaciones más importantes de esta ecuación ha sido predecir la existencia de “antipartículas” como los positrones. En particular, se ha comprobado experimentalmente que las energías de estas antipartículas (electrones y positrones) están íntimamente ligadas. Así, cuando un electrón de masa m tiene una energía en reposo E0=mc2, existe una antipartícula (positrón) que tiene una energía -E0. A esta propiedad se le conoce en la electrodinámica cuántica como “simetría conjugada”. Además, cuando la energía del electrón E >> E0, la energía es linealmente dependiente del momentum, E ~ k. Cuando estas partículas no tienen masa, este tipo de dispersión se conserva y los espectros de energía de ambas partículas convergen en un punto, como ocurre con los “conos de Dirac” en el grafeno.

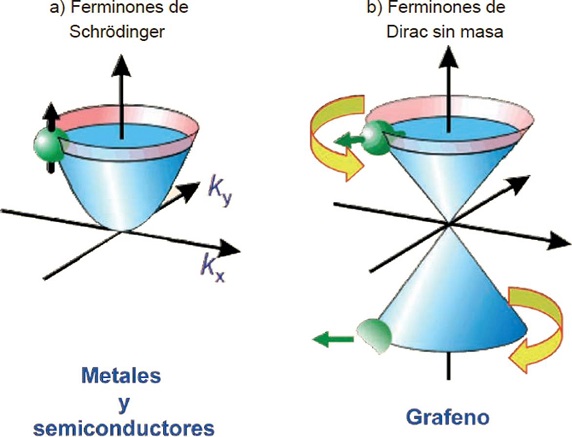
Otra similitud entre los portadores del grafeno y “los fermiones de Dirac sin masa” de la electrodinámica cuántica es la conexión entre el movimiento de estas partículas y la dirección de su espín. En ambos casos, el espín de la partícula (electrón) tiene la dirección del movimiento de propagación, y la “antipartícula” (hueco) la dirección opuesta del movimiento de propagación, tal y como se observa en la Figura 5. Esta situación es única en materiales, pues usualmente una partícula de espín ½ y masa m, como los electrones, pueden tener sólo espín hacia arriba y hacia abajo. Ésta es la conexión maravillosa con la electrodinámica cuántica: los portadores en el grafeno se comportan como partículas cargadas sin masa y sus espines tienen “simetría conjugada”. Este comportamiento de los electrones en un material no se había observado previamente y, más importante aún, podría ser aprovechado para innovaciones tecnológicas.

 

Figura 5. Representación esquemática de: a) las direcciones de espín de los portadores de carga en un metal o semiconductor y, b) en grafeno.

 

Propiedades de transporte

Velocidad de Fermi y masa ciclotrónica

La velocidad de Fermi es una de las cantidades que se deben controlar antes de diseñar dispositivos de alta movilidad. Esta cantidad está asociada a la energía de Fermi y es un concepto muy utilizado en física del estado sólido para caracterizar metales, semiconductores y aislantes. En particular, si extraemos toda la energía posible a una membrana de grafeno enfriándola cerca del cero absoluto (0 K), los portadores de carga aún se estarían moviendo sobre su superficie. Los electrones y huecos que se muevan más rápido lo harán a una velocidad máxima. Esta velocidad es la velocidad de Fermi y corresponde a la energía cinética de los portadores del último estado ocupado. La velocidad de Fermi se puede conocer experimentalmente de forma indirecta de un espectro arpes (Figura 4a) o teóricamente de la estructura de bandas calculada (Figura 4c). Como se mostró en ambos casos en grafeno, la relación entre E y k es lineal, y vF =dE/dk ≈ ×1 10−6.

Otra cantidad importante y que está relacionada con el movimiento de propagación de los portadores descritos en la sección anterior (Figura 5b) es la masa ciclotrónica. En los trabajos experimentales de Novoselov y colaboradores (Novoselov et al., 2005), se observó que la masa ciclotrónica (m*) depende de la densidad de electrones o huecos (n) como su raíz cuadrada 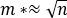. Por otro lado, considerando un modelo dentro de una aproximación semi-clásica (Ashcroft y Mermin, s/f), la masa ciclotrónica se puede expresar como

 
 

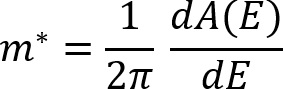
donde A(E) representa el área transversal de los conos de Dirac (Figura 5a) encerrada por la órbita en que se mueven los portadores de carga y está dada como

 
 

Sustituyendo esta expresión para A en la ecuación anterior para m*, tenemos que la masa ciclotrónica se puede expresar como,

 
 

Así, a partir de la velocidad de Fermi encontramos la dependencia de la razón m* / m0 como función de la densidad de portadores (Figura 6), donde mo es la masa del electrón libre. En la Figura 6, los círculos corresponden a las mediciones hechas por Novoselov (Novoselov et al., 2005) y las líneas sólidas a los valores obtenidos por cálculos de primeros principios (Cifuentes-Quintal et al., s/f). Éste es un buen ejemplo de que teoría y experimento pueden acompañarse para contestar una misma pregunta. Actualmente, buscamos diferentes procedimientos para modular la velocidad de Fermi y la masa efectiva de estos portadores, para sintonizar el transporte de estas partículas en dispositivos de alta velocidad. Las deformaciones mecánicas, la adsorción molecular, campo eléctrico aplicado, así como introducir impurezas o vacancias, son algunos de los mecanismos de modulación de portadores que se están explorando. También se estudian los efectos de tamaño finito en nanocintas y nanohojuelas de grafeno.

 

Figura 6. Masa ciclotrónica de los portadores de carga (electrones o huecos) en grafeno como función de su concentración (n). Los círculos azules corresponden a los datos experimentales que se midieron para los electrones y los círculos rojos para los huecos (Novoselov et al., 2005) Las líneas sólidas corresponden a las masas ciclotrónicas calculadas (Cifuentes-Quintal et al., s/f).

 

En resumen, el grafeno es un material que puede operar a escala nanométrica y a temperatura ambiente, con propiedades de transporte que ningún semiconductor ofrece. Por ello, todo apunta a que se podrán crear nuevos dispositivos electrónicos con base en este material. El principal reto para quienes lo estudiamos en forma experimental o teórica es ampliar el rango de modulación de estas propiedades.

Biblografía